Definizione 1.1 (Prodotto scalare).
 |
dove non diversamente specificato.
I vettori sono convenzionalmente intesi come vettori colonna† .
Gli oggetti grafici sono usualmente rappresentati come liste di punti; in generale una curva sarÓ rappresentata con
una matrice d×n† †In questo contesto d=2 o 3 .
Per migliorare l’efficienza le operazioni tra vettori sono implementate in modo da eseguire la stessa
operazione in blocco su liste di vettori di lunghezza arbitraria (ovvero punto a punto lungo una
curva).
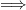 vw = 0 ⇔ v ⊥ w
vw = 0 ⇔ v ⊥ w
Su una base canonica: vw = ∑
viwi = vT w
Dati v(t),w(t):
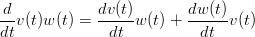 |
Dati v(t),w(t):
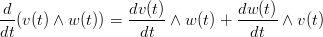 |
Casi particolari:
 |
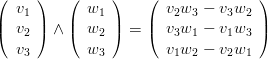 |
Una combinazione di punti:
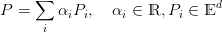 |
si dice baricentrica se ∑
iαi = 1, convessa se anche αi > 0∀i
Se la combinazione Ŕ baricentrica, pu˛ essere scritta come la somma di uno qualsiasi degli addendi e
un vettore:
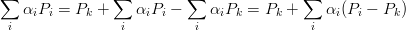 |
Una combinazione baricentrica convessa Ŕ utile per rappresentare parametrizzazioni di oggetti:
Esempio 1.1 (Punto medio di un segmento).
s = b0b1; b0,b1 ∈ℝ2;
M = ∑
i=1,2αibi = b0 + α0(b0 − b0) + α1(b1 − b0) = b0 + α1(b1 − b0); α1 = α2 = 
Esempio 1.2 (Punti di un segmento). Generalizzando l’esempio precedente:
s = b0b1; b0,b1 ∈ℝ2; t ∈ [0, 1];
P(t) = tb0 + (1 − t)b1 = b0 + (1 − t)(b1 − b0)
Definizione 1.3 (Spazio di lavoro). Si definisce spazio affine di ordine d, a partire da un punto O ∈ℝd, l’insieme:
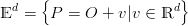 |
Definizione 1.4 (Convex Hull).
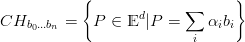 |
in cui gli αi formano una combinazione baricentrica convessa.
CH Ŕ il pi¨ piccolo insieme convesso che contiene i punti b0...bn
Generalmente si usano funzioni del tipo
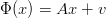 | (1.1) |
in cui A ∈Md×d e v ∈ℝd che sono lineari e permettono di definire facilmente le trasformazioni pi¨ comuni in grafica.
Traslazione La traslazione si ottiene con una funzione del tipo (1.1) in cui A ≡ I, per cui Φ(x) = x + v. Alternativamente Ŕ possibile modificare la matrice A:
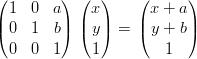 |
Rotazione La rotazione intorno all’origine (del sistema di riferimento ortonormale corrente) si ottiene ancora con una funzione del tipo (1.1) in cui v ≡ 0 (vettore nullo, non c’Ŕ traslazione) ed in cui la matrice, nel caso tridimensionale, assume la forma† :
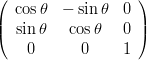 |
Scalatura La scalatura si ottiene imponendo un fattore di scala ad ogni dimensione della matrice identitÓ:
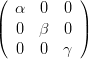 |
Le trasformazioni affini sono lineari rispetto alle combinazioni baricentriche. Infatti:
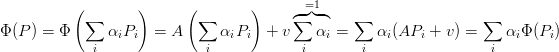 |
Inoltre, se A Ŕ ortogonale† †ATA = AAT = I ,
una trasformazione della famiglia (1.1) lascia invariati angoli e lunghezze.
Infatti, dati x,y vettori, per le lunghezze:
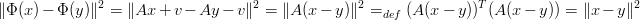 |
Per gli angoli, se x,y sono tali che xT y = |x||y| cos θ ed, in quanto vettori, possono essere letti come x = a − b; y = c − d (con a,b,c,d ∈ℝd):
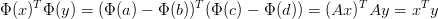 |
Definizione 1.6 (Curva). Si definisce curva l’immagine di un’applicazione X : I → Ed continua e localmente iniettiva.
Definizione 1.7 (Rappresentazione Parametrica). L’applicazione X : I → Ed continua e
localmente iniettiva si dice rappresentazione a parametri in I della curva; in generale una stessa
curva pu˛ ammettere pi¨ di una rappresentazione parametrica.† †Ad esempio, un segmento di retta (curva degenere) tra l’origine e il punto (1,1) pu˛ essere rappresentata
in forma implicita (ax + by + c = 0), esplicita (y = mx + q) o parametrica su un’intervallo I(= [0,1] per
esempio):
X(t) = 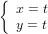 o equivalentemente X(t) =
o equivalentemente X(t) = 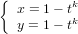
Definizione 1.8 (Rappresentazione parametrica differenziabile). La rappresentazione X(t) di dice differenziabile se esiste la funzione:
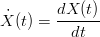 |
Se Ẋ≠0 su tutto l’intervallo di definizione I, X si dice differenziabile regolare
La non unicitÓ della rappresetazione parametrica suggerisce che si possa passare da una rappresentazione all’altra di una stessa curva, utilizzando di volta in volta la parametrizzazione con le caratteristiche pi¨ adatte al contesto.
Definizione 1.9 (Funzioni di riparametrizzazione). Sia τ : I → I2. Si definisce
riparametrizzazione di X rispetto a τ una funzione 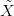 tale che
tale che 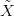 (τ(t)) = X(t).
(τ(t)) = X(t).
Si ha che:
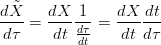 |
in cui dX∕dt Ŕ la tangente alla curva e dt∕dτ Ŕ uno scalare > 0.
Se τ ∈C1 e 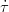 > 0 su tutto I la riparametrizzazione si dice ammissible; in questo caso la curva Ŕ
percorsa tutta nello stesso verso e la sua tangente non cambia verso nÚ direzione, ma solo il
modulo.
> 0 su tutto I la riparametrizzazione si dice ammissible; in questo caso la curva Ŕ
percorsa tutta nello stesso verso e la sua tangente non cambia verso nÚ direzione, ma solo il
modulo.
Osservazione 1.1 (Tangente alla curva). La tangente alla curva non pu˛ essere usata per
caratterizzarla, in quanto potenzialmente cambia modulo al cambiare della rappresentazione.
Per caratterizzare una curva occorre definire il versore tangente:
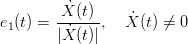 |
Definizione 1.10 (Rappresentazione parametrica regolare). Se Ẋ(t)≠0 ∀t ∈ I la rappresentazione parametrica si dice regolare.
La lunghezza dell’arco pu˛ essere usata come funzione di riparametrizzazione ammissibile, che ha
anche la caratteristica di essere lineare rispetto alle lunghezze sulla curva. In particolare
S : [a,b] → [0,l], e 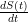 =
= 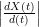 implica che se X(t) Ŕ regolare anche S(t) lo Ŕ, e vale
anche:
implica che se X(t) Ŕ regolare anche S(t) lo Ŕ, e vale
anche:
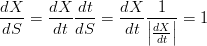 |
Osservazione 1.2 (Invarianza rispetto alla rappresentazione). La lunghezza dell’arco Ŕ invariante rispetto alla rappresentazione parametrica della curva, infatti, cambiando parametrizzazione:
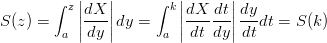 |
Definizione 1.12 (Fernet Frame). Il Frenet Frame Ŕ un sistema di coordinate ortonormali definito localmente in un punto di una curva X(t).
╚ possibile definire un Frenet frame† †L’insieme di tutti i Frenet frame Ŕ rappresentato tramite tre vettori ortonormali e1,e2,e3; in realtÓ ogniuno di essi Ŕ una funzione del parametro della rappresentazione della curva (C’Ŕ un Frenet frame diverso per ogni punto della curva). a partire dalle derivate di una qualsiasi rappresentazione parametrica X(t) di una curva:
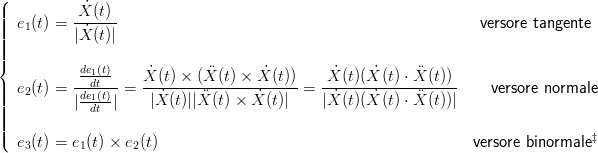 |
‡IdentitÓ “BAC-CAB”: A × (B × C) = B(A ⋅ C) − C(A ⋅ B).
La curvatura Ŕ una grandezza caratteristica della curva indipendente dalla sua rappresentazione
parametrica.
L’espressione della curvatura si semplifica notevolmente quando la rappresentazione Ŕ lunghezza
dell’arco:
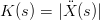 |
in quanto Ẋ(s) ≡ 1.
La torsione si annulla solo quando il prodotto misto Ŕ nullo:
![... [ ... ]
(X˙(t) × XĘ(t)) ⋅X (t) = det( X˙(t);XĘ(t);X (t)) = 0](tesi38x.png) |
La torsione Ŕ non nulla solo nello spazio e non su un piano.
Definizione 2.1 (Base di Bernstein). I polinomi di Bersntein sono una famiglia di polinomi definiti, per ogni n ∈ℕ+, come:
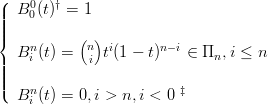 |
Definizione 2.2 (Polinomi di Bernstein in forma ricorsiva).
| B00 | = 1 | ||
| Bjn | = 0, j≠0, 1,...,n | ||
| Bin | = (1 − t)B in−1 + tB i−1n−1 |
Caso (i = 0 e i = n).
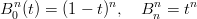 |
Caso (0 < i < n). in quanto 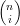 =
= 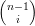 +
+ 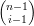 :
:
| Bin(t) | =  ti(1 − t)n−i = ti(1 − t)n−i = 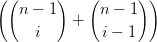 ti(1 − t)n−i ti(1 − t)n−i | ||
= (1 − t)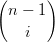 ti(1 − t)n−i−1 + t ti(1 − t)n−i−1 + t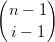 ti−1(1 − t)n−i ti−1(1 − t)n−i | |||
| = (1 − t)Bin−1 + tB i−1n−1 |
Definizione 2.3 (Polinomi di Berstein di grado n). Si definisce Polinomio di Bernstein di grado n la serie:
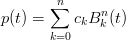 |
I polinomi di Bernstein sono definiti su tutto ℝ, ma ci si limita a studiarne le proprietÓ nell’intervallo [0, 1] (sufficiente in questo contesto).
Osservazione 2.1 (MappabilitÓ della base). I polinomi di Bernstein possono essere definiti, in maniera equivalente, su qualsiasi intervallo [a,b] mappabile a [0, 1]:
![( )
n n (t-−-1)i(b-−-t)n−i
B i (t) = i (b − a)n , t ∈ [a, b]](tesi52x.png) |
Ogni polinomio della base Ŕ non negativo in quanto prodotto di componenti non negative
(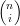 ,ti, (1 − t)n−i).
,ti, (1 − t)n−i).
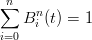 |
infatti, ∀t ∈ℝ:
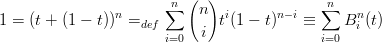 |
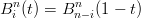 |
infatti:
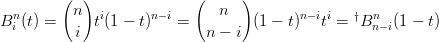 |
†Per il binomio di Newton vale la proprietÓ 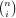 =
= 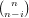
I polinomi di Bernstein sono una base per Πn; infatti, Bin pu˛ essere scritto come:
![( ) ( ) ( )
n n i n−i i n n∑−i n − i j n−i−j n−i− j
B i (t) = t(1 − t) = t [1 ] − 1 t
i i j=0 j](tesi61x.png) |
da cui:
 |
Se la matrice del cambio di base Ŕ non singolare i polinomi di Bernstein sono linearmente indipendenti; la matrice Ŕ non singolare in quanto triangolare superiore con tutti elementi non nulli sulla diagonale (determinante non nullo).
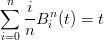 |
Infatti, per induzione su n:
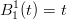 |
e supponendo che valga per n − 1:
∑
i=0n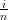 Bin(t) Bin(t) | = ∑
i=0n ![[ n−1 n− 1]
(1 − t)B i + tBi−1](tesi67x.png) | ||
= 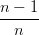 (1 − t) ∑
i=0n−1 (1 − t) ∑
i=0n−1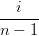 Bin−1(t) + t Bin−1(t) + t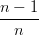 ∑
i=1n ∑
i=1n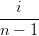 Bi−1n−1(t) Bi−1n−1(t) | |||
= 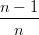 (1 − t)t + (1 − t)t + 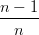 t∑
j=0n−1 t∑
j=0n−1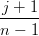 Bjn−1(t) = Bjn−1(t) = | |||
= 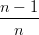 (1 − t)t + (1 − t)t + 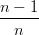 t t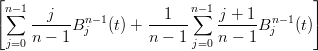 | |||
= 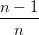 (1 − t)t + (1 − t)t + 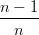 t t![[ ]
t + --1---
n − 1](tesi80x.png) = = | |||
= 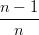 (1 − t)t + (1 − t)t + 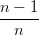 t2 + t2 +  = t = t |
Un polinomio di Bernstein p(t) = ∑ k=0nc kBkn(t) a coefficienti c 0,..,cn, dato V il numero di variazioni di segno della sequenza di costanti e N numero di radici reali di p(t) contate con la loro molteplicitÓ, gode della proprietÓ:
![N ≤ V, e N = V − 2k, t ∈ [0, 1].](tesi86x.png) |
Infatti,
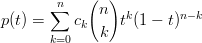 |
parametrizzato su u ∈ [0,∞], ovvero considerando t = 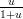 e (1 − t) =
e (1 − t) = 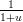 , diventa:
, diventa:
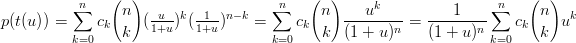 |
che Ŕ un polinomio sulla base canonica per il quale vale la regola di Cartesio† †Il numero di radici positive (contato con molteplicitÓ) Ŕ dato dal numero di cambi di segno (variazioni) fra due coefficienti consecutivi. .
| Bin(0) | = 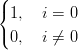 | ||
| Bin(1) | = 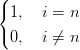 |
La derivata dei polinomi di Bernstein pu˛ essere espressa in termini della base di Bernstein stessa:
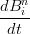 | = 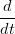 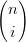 ti(1 − t)n−i = ti(1 − t)n−i = | ||
= 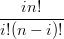 ti−1(1 − t)n−1 − ti−1(1 − t)n−1 −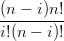 ti(1 − t)n−1−i ti(1 − t)n−1−i | |||
= n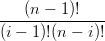 ti−1(1 − t)n−i − n ti−1(1 − t)n−i − n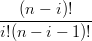 ti(1 − t)n−i−1 ti(1 − t)n−i−1 | |||
= n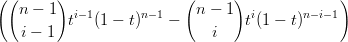 | |||
= n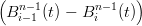 |
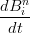 | = 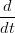 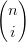 ti(1 − t)n−i ti(1 − t)n−i | ||
=  ti−1(1 − t)n−i−1[i(1 − t) − t(n − i)] ti−1(1 − t)n−i−1[i(1 − t) − t(n − i)] | |||
= 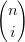 ti−1(1 − t)n−i−1[i − nt] ti−1(1 − t)n−i−1[i − nt] | |||
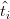 =
=  ,
con i = 0,…,n
,
con i = 0,…,n
Definizione 2.4 (Curva di BÚzier). Dati b0,...,bn ∈Ed insieme di punti di controllo, si definisce curva di BÚzier il polinomio:
![∑n n
X (t) = biBi (t), t ∈ [0, 1]
i=0](tesi110x.png) |
Definizione 2.5 (Poligono di controllo). Si definisce poligono di controllo il poligono che si ottiene unendo ordinatamente i punti di controllo.
La curva giace completamente nella convex hull dei punti di controllo, in quanto ogni punto della curva Ŕ una combinazione baricentrica di questi† †I polinomi di Bernstein partizionano l’unitÓ .
Segue direttamente dai valori agli estremi dei polinomi di Bernstein che X(0) ≡ b0 e X(1) ≡ bn.
Data Φ : Ed →Ed di tipo Φ(p) = Ap + v, si ha:
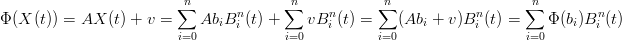 |
Le curve di BÚzier sono simmetriche rispetto all’ordine dei punti di controllo, infatti, dati ci = bn−i:
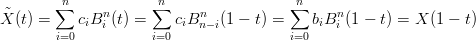 |
Se i punti di controllo sono allineati ed equidistanti la convex hull Ŕ il segmento b0bn e la curva giace su una retta:
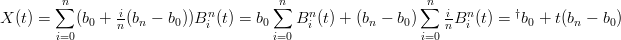 |
†Precisione lineare dei polinomi di Bernstein
Modificando uno dei punti di controllo b0,...,bn:
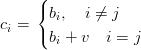 |
si ottiene:
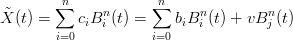 |
ovvero tutti i punti della curva si spostano nella direzione di v con un’incidenza che dipende da t e dalla forma del j−esimo polinomio di Bernstein. In generale, in quanto i polinomi hanno una forma a campana, i punti della curva sono interessati in maniera proporzionale alla distanza dal punto di controllo modificato.
La proprietÓ di variation diminishing aiuta a capire l’andamento della curva; si pu˛ infatti sapere il
numero massimo di intersezione che la curva pu˛ avere con una retta (N) a partire da quello del
poligono di controllo (Np). In particolare, N ≤ Np e N = Np − 2k.
Sia r = αx + βy + γ, le intersezioni si possono ricavare, separando le dimensioni, con
l’equazione:
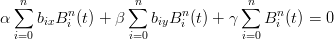 |
da cui:
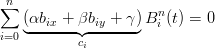 |
e la proprietÓ segue direttamente da quella di variation diminishing dei polinomi di Bernstein.
| Ẋ(t) | = ∑
i=0nb
iBin(t) = n∑
i=0nb
i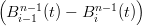 | ||
= n![[ n−1 n−1]
(b1 − b0)B 0 (t) + ...+ (bn − bn− 1)B n−1](tesi123x.png) | |||
| = n∑ i=0n−1(b i+1 − bi)Bin−1(t) = n∑ i=0n−1Δb iBin−1(t) |
dove Δbi = def(bi+1 − bi).
La derivata di una curva di BÚzier Ŕ quindi ancora una curva dello stesso tipo ma di grado minore e
con punti di controllo differenti.
Dalla forma della derivata seconda:
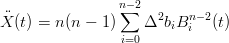 |
si pu˛ generalizzare† †Falling factorial: xk = x(x − 1)...(x − k + 1), ovvero i primi k termini del fattoriale. Nota: xk = 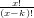 :
:
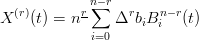 |
In quanto:
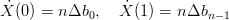 |
la curva di BÚzier Ŕ sempre tangente ai segmenti che uniscono i primi e gli ultimi due punti del poligono di controllo.
I punti della curva possono essere calcolati ricorsivamente definendo:
 |
Si dimostra per induzione che questa formula ricorsiva, in r passi, calcola i punti della curva. Per r = 1:
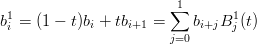 |
Supponendo che valga per r − 1, si ha:
| bir(t) | = (1 − t)b ir−1(t) + tb i+1r−1(t) | ||
| = (1 − t) ∑ j=0r−1b i+jBjr−1(t) + t∑ j=0r−1b i+j+1Bjr−1(t) | |||
| = (1 − t) ∑ k=ii+r−1b kBk−ir−1(t) + t∑ k=i+1i+rb kBk−i−1r−1(t) | |||
= ∑
k=ii+r![[ ]
(1 − t)bkBrk−− 1i(t) + tbkBrk−−1i−1(t)](tesi133x.png) | |||
| = ∑ k=ii+rb kBk−ir(t) = ∑ j=0rb j+iBjr(t) |
Una curva di BÚzeier Ŕ rappresentabile con un’altra di grado pi¨ elevato, ovvero esiste soluzione all’equazione:
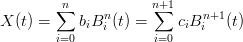 |
Per la proprietÓ di interpolazione agli estremi si deve avere c0 = b0 e cn+1 = bn.
Moltiplicando a sinistra per (t + (1 − t)) e usando la proprietÓ di partizionamento dell’unitÓ dei
polinomi di Bernstein, si ha:
![n∑ ∑n ( ) [ ] n∑+1
(t + (1 − t)) biBn (t) = bi n ti(1 − t)n−i+1 + ti+1(1 − t)n−i = ciBn+1 (t)
i=0 i i=0 i i=0 i](tesi135x.png) |
da cui, considerando b−1 = bn+1 = 0:
∑
i=0nb
i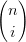 ![[ ]
ti+1(1 − t)n−i + ti(1 − t)n− i+1](tesi137x.png) | |||
= ∑
i=0nb
i ti+1(1 − t)n−i + ∑
i=0nb
i ti+1(1 − t)n−i + ∑
i=0nb
i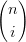 ti(1 − t)n−i+1 ti(1 − t)n−i+1 | |||
= ∑
i=0n+1b
i−1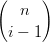 ti(1 − t)n−i+1 + ∑
i=0n+1b
i ti(1 − t)n−i+1 + ∑
i=0n+1b
i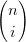 ti(1 − t)n−i+1 ti(1 − t)n−i+1 | |||
= ∑
i=0n+1![[( ) ( ) ]
ni−1 bi−1 + ni bi
------(n+1)-------
i](tesi142x.png) Bin+1(t) Bin+1(t) |
![[( n ) (n) ]
i−1 bi−1 + i bi i ( i )
ci = -------(n+1)------ = n-+-1bi−1 + 1 − n-+-1- bi
i](tesi143x.png) |
Osservazione 2.2. I punti di controllo ci sono ottenuti come combinazione lineare dei due vertici adiacenti del poligono di controllo di partenza, quindi il nuovo poligono Ŕ inscritto nel vecchio.
Osservazione 2.3 (Repeated degree elevation). Per disegnare una curva si pu˛ pensare di innalzare il grado del poligono di controllo finnchŔ questo non sia sufficientemente vicino alla curva; i coefficienti dell’r-esima iterazione sono:
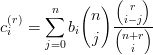 |
Fissato t, se r →∞ il poligono tende effettivamente alla curva, ma il costo computazionale Ŕ molto pi¨ elevato dell’algoritmo di de Casteljau in quanto servono molte elevazioni per raggiungere una precisione paragonabile.
Una curva pu˛ essere suddivisa in due curve dello stesso grado giunte in un punto.
Dati 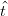 ∈]0, 1[ e:
∈]0, 1[ e:
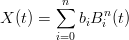 |
si cercano:
![( ∑n t
||||CL (τ) = ckBnk(τ ) = X (t),t ∈ [0,^t],τ = - ∈ [0,1]
{ k=0 ^t
|| n∑ n t − ^t
||(CR (u ) = dkB k(τ) = X (t),t ∈ [^t,1],u = 1-−-t ∈ [0,1]
k=0](tesi149x.png) |
Definizione 2.6 (Operatori identitÓ e shift).
Si definiscono gli operatori I,E tali che Ibi = bi,Ebi = bi+1.
Osservazione 2.4 (Rappresentazione alternativa delle curve di BÚzier). I punti della curva di
BÚzier (algoritmo di de Casteljau) si possono rappresentare a partire dagli operatori shift e
identitÓ: bir = ![[(1 − t)I + tE ]](tesi150x.png) r−1b
i.
r−1b
i.
I coefficienti ck e dk si ottengono dall’algoritmo di de Casteljau come:
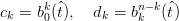 |
infatti† †Il caso CR si dimostra in maniera analoga :
| CL(τ) | = ∑
k=0nb
0k( ) )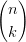 τk(1 − τ)n−k τk(1 − τ)n−k | ||
= ∑
k=0n![[ ]
(1 − ^t)I + ^tE](tesi154x.png) kb
0 kb
0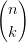 τk(1 − τ)n−k τk(1 − τ)n−k | |||
= ∑
k=0n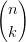 τk τk![[ ^ ^ ]
(1 − t)I + tE](tesi157x.png) k(1 − τ)n−kIn−kb
0 k(1 − τ)n−kIn−kb
0 | |||
= ∑
k=0n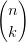 ![[τ 1 − τ ^tI + τ ^tE ]](tesi159x.png) k k![[(1 − τ )I ]](tesi160x.png) n−kb
0 n−kb
0 | |||
= ![[ ]
τI − τ^tI + τ^tE + I − τ I](tesi161x.png) nb
0 nb
0 | |||
= ![[ ^ ^ ]
(1 − t)I + tE](tesi162x.png) nb
0 nb
0 |
Le curve di BÚzieri razionali sono un’estensione alle curve di BÚzier che mira a migliorarne la controllabilitÓ.
Un insieme Ŕ rappresentabile mediante coordinate omogenee se Ŕ possibile associare un vettore numerico (x1,...,x2) ad ogni elemento dell’insieme, in modo tale che due vettori distinti siano associati a due oggetti diversi solo se linermente indipendenti.
Definizione 2.7 (Spazio proiettivo). Lo spazio proiettivo P(K) associato ad uno spazio vettoriale K Ŕ definito come l’insieme dei suoi sottospazi vettoriali di dimensione uno (rette).
Se ogni vettore di uno spazio vettoriale di dimensione finita Ŕ rappresentabile tramite le sue coordinate (x1,...,xn), ogni retta Ŕ descrivile come lo span lineare di un vettore non nullo: λ(x1,...,xn).
Interpretazione geometrica in d = 3 Si immagini un piano E2 immerso in uno spazio E3 ed allineato col sistema di riferimento, ad esempio perpendicolare all’asse z. I punti di E3 sono rappresentabili tramite l’insieme delle triple (x,y,z) oppure, a partire dai punti di E2, come unione dei punti al finito ed i punti all’infinito:
![{ 2} { 2 }
[x,y,1]|(x,y) ∈ E ∪ [x,y,0 ]|(x,y) ∈ P (E )](tesi167x.png) |
Analogamente Ŕ possible rappresentare i punti del piano a partire dai punti dello spazio attravero
un’operazione di proiezione: (x,y,z) → ( ,
,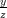 , 1).
, 1).
Curve di BÚzier razionali
Una curva di BÚzier razionale in uno spazio Ed Ŕ la proiezione di
una curva di BÚzier classica definita in uno spazio Ed+1. In particolare si
definisce† †Per comoditÓ di notazione si intende lo spazio proiettivo perpendicolare alla prima componente del vettore, ovvero
(x,y,z,...,cn) → (1,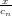 ,
,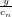 ,...) :
,...) :
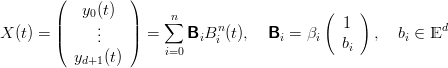 |
in cui i Bi sono vettori in Ed+1. La prima componente della curva (d + 1)-dimensionale Ŕ pertanto:
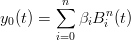 |
ed applicando direttamente il concetto di proiezione si ottiene la curva proiettiva in Ed:
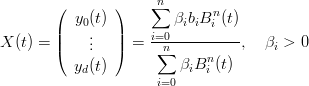 |
Osservazione 2.5. Se β0 = β1 = ... = βn, X(t) ≡ ∑ i=0nb iBin(t) ovvero rimane una BÚzier definita dai punti di controllo bi.
Sia s = 1 − t. La proprietÓ segue direttamente da quella dei polinomi di Bernstein:
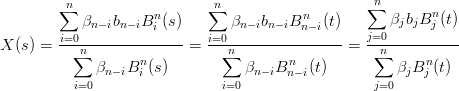 |
Definendo la curva come:
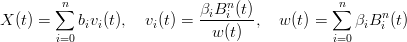 |
si ha che:
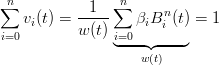 |
ovvero la curva Ŕ una combinazione convessa dei punti di controllo ed appartiene alla convex hull di questi.
Deriva direttamente dal fatto che la curva Ŕ una combinazione baricentrica di punti; la dimostrazione Ŕ analoga a quella per le curve di bÚzier classiche.
In generale non vale, infatti:
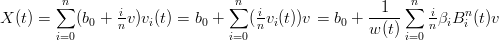 |
da cui:
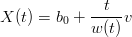 |
Se i βi sono omogenei per˛ la proprietÓ si mandiene valida.
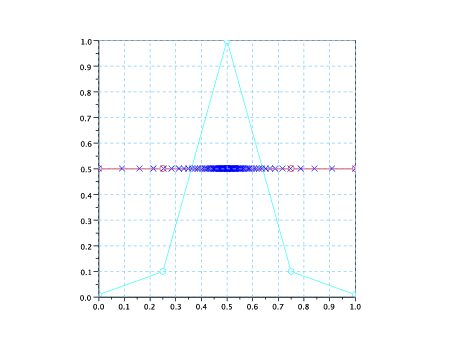
La curva interpola i punti di controllo agli estremi:
| X(0) | = 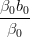 = b0 = b0 | ||
| X(1) | = 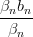 = bn = bn |
I punti della curva X(t) = ∑
i=0nb
ivi(t), con vi(t) = 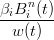 ,w(t) = ∑
i=0nβ
iBin(t), che giacciono
sulla retta ax + by + c = 0 sono:
,w(t) = ∑
i=0nβ
iBin(t), che giacciono
sulla retta ax + by + c = 0 sono:
| a∑ i=0nb ixvi(t) + b∑ i=0nb iyvi(t) + c∑ i=0nv i(t) | = 0 | ||
| ∑ i=0n(ab ix + bbiy + c)vi(t) | = 0 | ||
∑
i=0n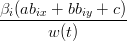 Bin(t) Bin(t) | = 0 |
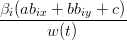 si rientra nel caso della curve di BÚzier classica, per cui la
proprietÓ Ŕ dimostrata.
si rientra nel caso della curve di BÚzier classica, per cui la
proprietÓ Ŕ dimostrata.
Modificando uno dei pesi:
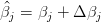 |
si ottiene la curva:
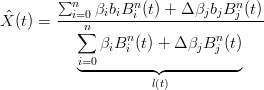 |
Confrontando la curva modificata con quella originale si ha:
(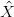 (t) − X(t))l(t) (t) − X(t))l(t) | = ∑ i=0nβ ibiBin(t) + Δβ jbjBjn(t) −∑ i=0nβ ibiBin(t) − X(t)Δβ jBjn(t) | ||
| = ΔβiBin(t)[b j − X(t)] |
![Δ βiBni (t)
( ^X (t) − X (t)) = ∑n------n------------n--[bj − X (t)]
i=0 βiBi (t) + Δ βjBj (t)](tesi189x.png) |
Modificando un peso si ha quindi un effetto su ogni punto della curva, direttamente proporzionale alla distanza bj − X(t): la curva tende ad avvicinarsi al punto bj se Δβj Ŕ positivo, allontanarsi altrimenti.
Sia:
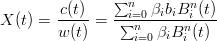 |
Si pu˛ calolare la derivata di X(t):
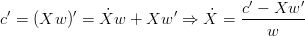 |
Le derivate di c(t) e w(t) sono note:
| c(r) | = nr ∑ i=0n−rΔrβ ibiBin−r | ||
| w(r) | = nr ∑ i=0n−rΔrβ iBin−r |
![[∑ (∑ ) ]
n ni=−0rΔ βibiBni −r(t) − ni−=r0 ΔβiBni−r(t) X (t)
X˙(t) = ------------------∑n-------n---------------------
i=0βiB i (t)](tesi193x.png) |
La tangenza agli estremi Ŕ mantenuta, infatti:
| Ẋ(0) | = n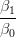 Δb0 Δb0 | ||
| Ẋ(1) | = n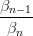 Δbn−1 Δbn−1 |
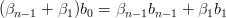 |
Definizione 2.8 (Curva di BÚzier razionale in forma standard). Una curva di BÚzier razionale si dice in forma standard se i pesi associati agli estremi del poligono di controllo sono unitari.
Per trasformare una curva razionale in una in forma standard, si utilizza la riparametrizzazione:
![t = (1-+-α-)u- ≡ ϕ(u), α ∈ ℝ, u ∈ [0,1 ]
1 + αu](tesi198x.png) |
La derivata della funziona di riparametrizzazione ϕ(u) vale:
![1 1 + α
ϕ ′(u) = --------2 [(1 + α)(1 + α) − α(1 + α )u ] =--------2-
(1 + αu ) (1 + αu )](tesi199x.png) |
quindi la funzione Ŕ monotona per α > −1, e la riparametrizzazione Ŕ ammissibile in quel
range.
Ha senso quindi applicarla:
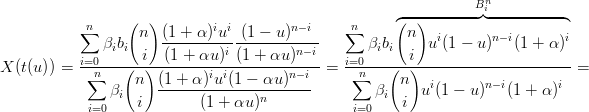 |
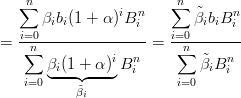 |
e richiedere che siano verificate:
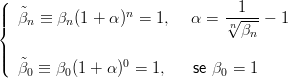 | (2.1) |
La forma standard si pu˛ ottenere solo nel caso in cui la condizione β0 = 1 sia giÓ verificata inizialmente.
Le sezioni coniche sono rappresentabili utilizzando curve di BÚzier di secondo grado.
Un punto p che giace nella convex hull di altri tre (b0,b1,b2)† †ogniuno ha componenti xi,yi che delimitano un triangolo Ŕ identificabile univocamente con un sistema di coordinate baricentriche (u0,u1,u2) a riferimenti b0,b1,b2:
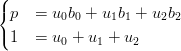 |
Il sistema di coordinate sopra descritto Ŕ univocamente determinato, si dimostra che in:
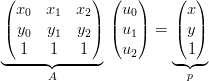 |
la matrice A Ŕ nonsingolare e quindi il sistema ammette soluzione unica. Il determinante di A Ŕ legato all’area del triangolo b0b1b2; fissando una base per esso si ha:
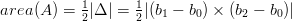 |
Applicando il metodo ci Cramer:
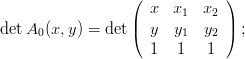 |
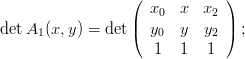 |
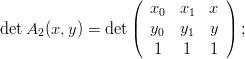 |
e quindi:
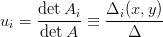 |
dove Δi = det Ai(x,y) e Δ = det A. Il determinante di A Ŕ non nullo quindi le ui sono tutte definite. Il sistema perde per˛ l’unicitÓ nel caso in cui tutti e tre i punti siano allineati.
In generale una curva conica Ŕ rappresentabile come:
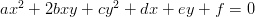 |
o in forma matriciale, dato il punto p = 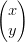 :
:
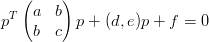 |
Il determinante della matrice determina il carattere della conica:
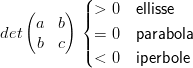 |
Si ricordano alcune definizioni:
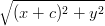 + + 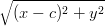 | = R, fuochi allineati sull’asse x e centro nell’origine | ||
 |
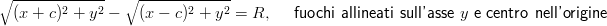 |
Siviluppando la formula di una curva di BÚzier razionale in forma standard di secondo grado e etichettandone in modo opportuno i termini:
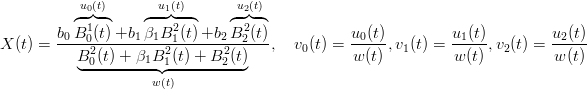 |
i punti della curva possono essere espressi in maniera semplice come:
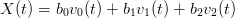 |
Dalle proprietÓ dei polinomi di Bernstein segue direttamente che ∑
vi(t) = 1 ovvero ogni punto della
curva Ŕ una combinazione baricentrica dei tre punti di controllo, leggibile anche come coordinate
baricentriche rispetto agli stessi.
Calcolando il quadrato della componente v1 si ottiene:
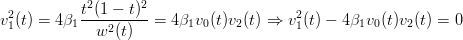 |
sostituendo ai vi la relativa notazione risultante dal teorema di Cramer vista nella sezione precedente (vi = Δi(x,y)∕Δ), si ha che punti della curva rispettano:
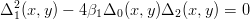 |
che un’equazione di secondo grado, ovvero una curva conica che cambia comportamento in base al valore di β1:
 |
Uno dei possibili modi per migliorare la controllabilitÓ e localitÓ di una curva di BÚzier Ŕ quello di considerare sottointervalli della curva come curve separate, preoccupandosi di gestire i raccordi. Dato un intervallo di definizione della curva [a,b] ed una sua partizione in m sottointervalli τ : a ≡ u1 < u2 < ... < um < um+1 ≡ b disgiunti ed adiacenti, si definisce la curva polinomiale a tratti:
![d ⋃
X (u) : [a, b] → E , X (u ) = Xi (t),t ∈ [ui,uu+1 )](tesi224x.png) |
in cui:
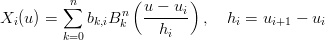 |
e bk,i Ŕ il k-esimo punto di controllo della curva i-esima. I punti della curva X(ui) sono detti nodi (knot) o punti di giunzione. La condizione di continuitÓ si ottiene imponendo:
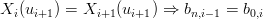 |
grazie alla proprietÓ di end-point interpolation; ad esempio date due curve disconnesse si pu˛ aggiungere un punto a tutte e due che stia spazialmente tra l’ultimo della prima e il primo della seconda.
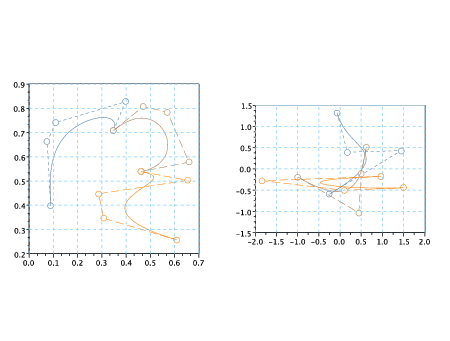
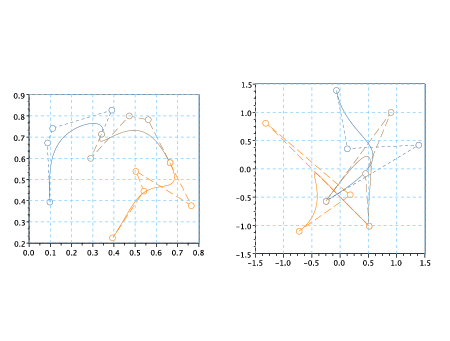
Per aumentare la regolaritÓ della curva si pu˛ voler imporre la continuitÓ delle derivate; ad esempio per ottenere una curva in C1 si impone:
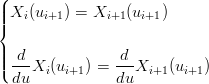 |
Si ha che:
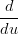 Xi(ui+1) = Xi(ui+1) = 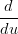 Xi+1(ui+1) Xi+1(ui+1) | |||
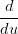 Xi(1) Xi(1)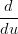 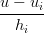 = = 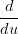 Xi+1(0) Xi+1(0)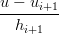 | |||
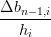 = = 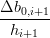 |
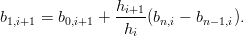 |
Analogamente per avere continuitÓ C2 si impone anche:
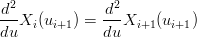 |
da cui:
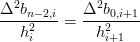 |
ovvero:
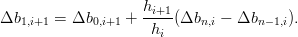 |
Quanto appena descritto Ŕ un metodo per ottenere una curva di BÚzier definita a tratti
parametrizzata in modo tale che rispetto al parametro u la velocitÓ di percorrenza della curva sia
proporzionale alla dimensione dei diversi intervalli assegnati ad ogni curva. In pratica Ŕ
comodo considerare l’intervallo [a,b] suddiviso equamente tra i vari tratti di curva (curva
polinomiale a tratti uniformi); in questo caso la funzione di riparametrizzazione Ŕ la stessa per
tutte (a meno dell’intervallo) e non c’Ŕ bisogno di riparametrizzarle, perchŔ si pu˛ dare per
scontato che ogni curva sarÓ valutata in [0, 1] quando u Ŕ nell’intervallo corrispondente. Si ha
che:
Le derivate delle due curve sono facili da derivare:
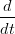 Xi(t) Xi(t) | = 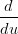 Xi+1(u) Xi+1(u) | ||
| n∑ k=0n−1Δb k,iBkn(t) | = m∑ k=0m−1Δb k,i+1Bkn(u) |
| n∑ k=0n−1Δb k,iBkn−1(1) | = m∑ k=0m−1Δb k,i+1Bkn−1(0) | ||
| nΔbn−1,i | = mΔb0,i+1 |
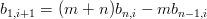 |
Analogamente per avere C2
| n(n − 1) ∑ k=0n−2Δ2b k,iBkn−2(1) | = m(m − 1) ∑ k=0m−2Δ2b k,i+1Bkn−2(0) | ||
| n(n − 1)Δ2b n−2,i | = m(m − 1)Δ2b 0,i+1 |
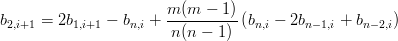 |
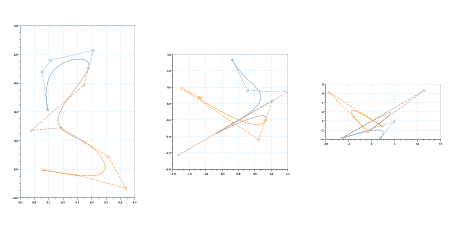
Due curve si raccordano con continuitÓ geometrica Gs nel punto p se esiste una riparametrizzazione
ammissibile per cui le curve hanno continuitÓ Cs in p.
Per avere continuitÓ G1, date due curve X(u),Y (t) e la funzione u(t) : [t
0,t1] → [u0,u1]:
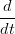 X(t1) = X(t1) = 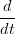 Y (t1) Y (t1) | |||
ω1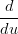 X(u1) = X(u1) = 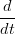 Y (t1), ω1 = Y (t1), ω1 = 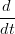 u(t1) > 0 u(t1) > 0 |
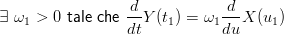 |
Il caso G2 Ŕ analogo:
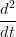 X(t1) = X(t1) = 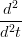 Y (t1) Y (t1) | |||
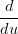 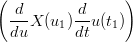 = = 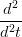 Y (t1) Y (t1) | |||
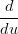 X(u1) X(u1)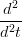 u(t1) + u(t1) + 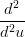 X(u1) X(u1)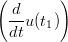 2 = 2 = 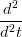 Y (t1) Y (t1) |
 |
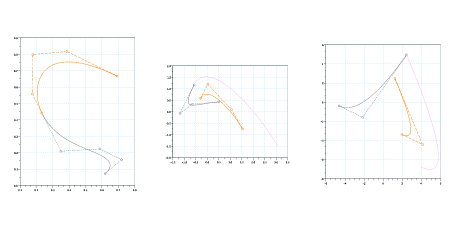
Come prima, nel caso pratico considerando equiparametrizzate le curve si ottiene, per le continuitÓ G1 e G2:
nΔbn−1,i = ω1mΔb0,i+1 → b1,i+1 = 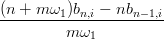 | |||
| n(n − 1)Δ2b n−2,i = m(m − 1)Δ2b 0,i+1 → b2,i+1 = | |||
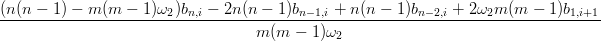 |
Vedi appendice A.1.
In generale, una curva SPLINE monovariata Ŕ una funzione S : [a,b] →ℝd polinomiale a tratti. In particolare, definita una partizione τ dell’intervallo [a,b]:
![⋃
[a,b] = Ii, Ii = [τi,τi+1), τ : a ≡ τ1 < τ2 < ...< τn < τn+1 ≡ b](tesi269x.png) |
Ii ∩ Ij = ∅ con i≠j, Ii ∪ Ii+1 ≡ [ti,ti+2) la funzione S Ŕ rappresentabile come:
![⋃ d
S = Pi, Pi : [τi,τi+1] → ℝ , Pi ∈ Πm](tesi270x.png) |
Si indica con Sm,τ una generica funzione SPLINE sulla partizione τ e composta di polinomi tutti di grado m. Considerando l’intervallo [a,b] suddiviso in n sottointervalli, si Ŕ definito uno spazio di dimensione:
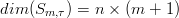 |
in quanto ogni polinomio di grado m Ŕ identificato da m+1 coefficienti. In pratica, volendo rappresentare una curva, si vuole che S sia continua (ovvero lim t→ti+1Pi(t) = Pi+1(ti+1)) e che anche le derivate si raccordino (S ∈Cm−1)† ; questo lascia uno spazio di dimensione:
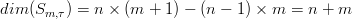 |
infatti ci sono n − 1 punti di raccordo per ogniuno dei quali si impogono m condizioni di di raccordo (una di continuitÓ e le derivate).
Si definiscono:
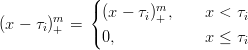 |
Definizione 3.1 (Base delle potenze troncate). Sulla partizione τ : a ≡ τ1 < ... < τl ≡ b si definisce base delle potenze troncate l’insieme di polinomi:
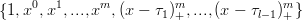 |
Teorema 3.1. L’insieme delle potenze troncate Ŕ una baste per lo spazio delle spline Sm,τ.
Dimostrazione. Si deve dimostrare che i polinomi della base sono l + m linearmente indipendenti, ovvero che:
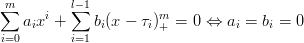 |
Se x ∈ I1 ≡ [τ1,τ2] si ha:
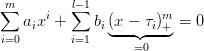 |
ovvero la tesi Ŕ dimostrata in quanto la base Ŕ quella canonica. Per x ∈ I2 si ha:
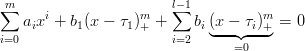 |
ma la propritÓ vale per gli ai, il che implica che debba valere anche b1. Procedendo allo stesso modo si dimostra la tesi per tutti i bi __
La base delle potenze troncate presenta problemi di malcondizionamento; questi possono essere risolti
definendo, sullo stesso concetto, una base a supporto compatto.
Si definisce una partizione di [a,b]† †vettore dei nodi
pi¨ rilassata della precedente:
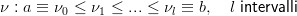 |
e, data la base:
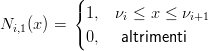 |
si definisce ricorsivamente:
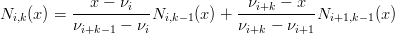 |
Nota (Abuso di notazione). Per comoditÓ, se uno dei denominatori di un termine in Ni,k(x) si annulla, questo viene considerato nullo.
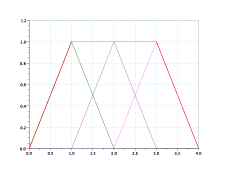 (a) k=2
(a) k=2 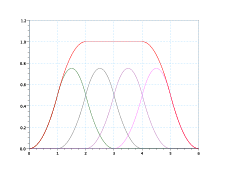 (b) k=3
(b) k=3
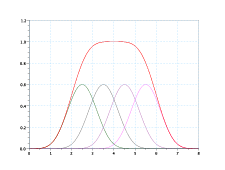 (c) k=5
(c) k=5 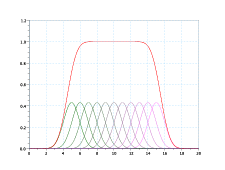 (d) k=10
(d) k=10
Ni,k(x) Ŕ a supporto compatto, infatti Ni,k = 0 se t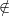 [ti,ti+k].
[ti,ti+k].
Ni,k(x) ≥ 0∀t ∈ [ti,ti+k], in quanto somma di soli termini positivi in quell’intervallo.
![∑n
Ni,k(t) = 1∀t ∈ [νk− 1,νn+1 ]
i=0](tesi289x.png) |
Per induzione, la tesi Ŕ vera banalmente per Ni,1(t) e t ∈ [t0,tn+1]; supponendola vera per Ni,k−1(t) , t ∈ [νk−2,νn+1] per Ni,k(t) e t ∈ [νk−1,νn+1] vale:
| ∑ i=0nN i,k(t) | = ∑
i=0n![[ t − νi νi+k − t ]
-----------Ni,k−1(t) + -----------Ni+1,k−1(t)
νi+k−1 − νi νi+k − νi+1](tesi290x.png) | ||
= 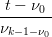 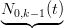 ≠0⇔t∈[ν0,νk−1] + ∑
i=1n ≠0⇔t∈[ν0,νk−1] + ∑
i=1n![[ ]
t − νi νi+k−1 − t
-----------+ -----------
νi+k−1 − νi νi+k− 1 − νi](tesi293x.png) Ni,k−1(t) Ni,k−1(t) | |||
+ 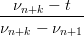 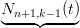 ≠0⇔t∈[νn+1,νn+k−1] ≠0⇔t∈[νn+1,νn+k−1] | |||
= 0 + ∑
i=1nN
i,k−1(t) + 0 + 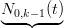 =0,t∈[νk−1,νn+1] =0,t∈[νk−1,νn+1] | |||
| = ∑ i=0nN i,k−1(t) |
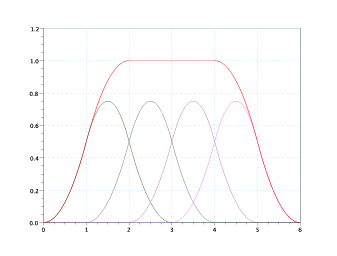
La derivata della base delle B-SPLINE Ŕ definita come segue:
![[ ]
dNi,k(x) = (k − 1) Ni,k−1(x)--− Ni+1,k−1(x)
dx νi+k− 1 − νi νi+k − νi+1](tesi298x.png) |
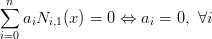 |
si verifica banalmente, ∀t ∈ [a,b]. Analogamente, se k = 2:
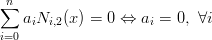 |
infatti nei nodi (x = νj) solo Nk−1,2(νj)≠0 e aj deve essere diverso da zero, per ogni j. Per dimostrare la proprietÓ per k > 2 occorre procedere per induzione, utilizzando i precedenti come casi base. Tenendo conto che vale:
![∑n ∑n [ N (x) N (x)]
aiNi,k(x) = 0 ⇒ (k − 1) ai ---i,k−1---- − --i+1,k−1--- = 0
i=0 i=0 νi+k−1 − νi νi+k − νi+1](tesi301x.png) |
espandendo e risommando i termini della sommatoria nella derivata si ottiene:
![n∑ [ a − a ]
(k − 1) ---i----0-- Ni,k−1(x) = 0
i=1 νi+k−1 − νi](tesi302x.png) |
da cui si deve avere ai = ai+1 ovvero tutti i coefficienti coincidenti. Riportando questo risultato alla sommatoria di partenza:
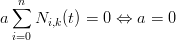 |
in quanto gli Ni,k(x) sono una combinazione baricentrica.
La definizione di SPLINE data nella sezione precedente richiede che la curva abbia lo stesso tipo di
continuitÓ su tutti i nodi. Questo vincolo nella pratica pu˛ essere troppo stringente, e talvolta conviele
usare uno spazio delle spline allargato.
Data la partizione:
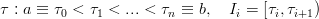 |
ed un vettore:
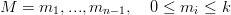 |
Questo vettore sta ad indicare il tipo di raccordo che si vuole nei punti τ2,..,τn, se mi = 0 non si chiede neanche la continuitÓ, se mi = s si chiede la continuitÓ delle derivate dalla zeresima alla s. Si definisce:
Sm,τ,M =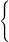 f : [a,b] →ℝd per cui f : [a,b] →ℝd per cui | ∃ p 1(t),...,pn(t) ∈ Πm,f(t)|Ii = pi(t), e | ||
| pi−1(s)(τ i) = pi(s)(τ i),s = {0,...,mi − 1} se mi > 0, | |||
nessuna condizione imposta in τi se mi = 0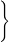 |
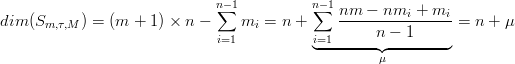 |
Per comoditÓ, usualmente il vettore M non si riferisce direttamente al grado di derivabilitÓ nei nodi, ma indica direttamente la molteplicitÓ del nodo i-esimo nel vettore dei nodi, e prende il nome di vettore delle molteplicitÓ. In una curva di grado k la molteplicitÓ del nodo (m) e il grado di derivabilitÓ della curva (d) sono legate dalla relazione:
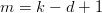 | (3.1) |
ovvero per ottenere una curva a derivabilitÓ massima (che coincide con le B-SPLINE classiche) la molteplicitÓ dei nodi deve essere minima (1) e viceversa, per ottenere la derivabilitÓ minima (nel caso pratico si richiede sempre la continuitÓ C0) la molteplicitÓ Ŕ massima (k).
Definizione 3.2 (Vettore dei nodi esteso). A partire dall’insieme M e dal vettore dei nodi ν (che ha n intervalli) si definisce il vettore dei nodi esteso† :
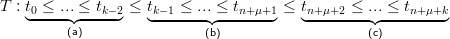 |
in cui:
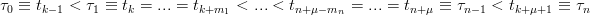 |
Come prima, si definisce ricorsivamente la base per le spline:
| Ni,1(t) | =  | ||
| Ni,k(t) | = 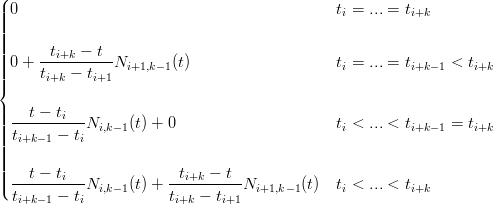 |
Osservazione 3.2 (Caso particolare: polinomi di Bernstein).
Ponendo [τ0,τ1] = [0, 1], il vettore dei nodi estesi per una spline di grado k diventa:
t : τ0 = t0 = ... = tk−1 < tk = ... = t2k−1 = τ1.
Dalla definizione di Ni,k, per i < k segue:
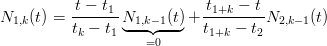 |
quindi, ricorsivamente:
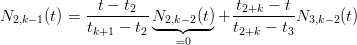 |
Si pu˛ scrivere la formula generica:
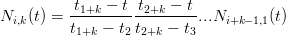 |
ma t0 = ... = tk−1 e tk = ... = t2k−1 da cui:
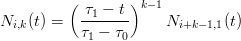 |
analogamente, per i ≥ k:
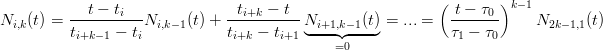 |
Da qui, sostituendo τ0 = 0 e τ1 = 1 si ottiene:
![N (t) = (1 − t)k−1 ≡ Bk −1(t), N (t) = tk− 1 ≡ Bk− 1, t ∈ [τ ,τ ]
1,k 1 k,k k−1 0 1](tesi319x.png) |
In generale si pu˛ dimostrare che:
![k−1
Ni+j,k(t) = B k (s), t ∈ [ti+j,ti+j+1],s ∈ [τ0,τ1]](tesi320x.png) |
La definizione di derivata Ŕ l’estensione diretta di quella della base B data in precedenza:
![[ ]
dNi,k(t) Ni,k− 1(t) Ni+1,k−1(t)
--------= (k − 1) ---------- − -----------
dt ti+k− 1 − ti ti+k−ti+1](tesi321x.png) |
La proprietÓ di somma unitaria della B-base estesa in [tk−1,tn+1] permette di utilizzarla in modo analogo ai polinomi di Bernstein per definire una curva:
![∑n
X (t) = diNi,k(t), t ∈ [tk−1,tn+1]
i=0](tesi324x.png) |
in cui di sono punti in Ed.
Invarianza alle trasformazioni affini
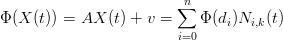 |
Controllo locale Se t ∈ [tr,tr+1]:
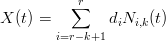 |
in quanto tutte le altre Ni,k(t) sono nulle, ne consegue che la modifica di di ha effetti sulla curva solo nel corrispondente intervallo ti,ti+k.
Strong ConvexHull Come nel caso dei polinomi di Bernstein, la somma ∑ i=0nd iNi,k(t), t ∈ [tk−1,tn+1] Ŕ una combinazione baricentrica dei di, quindi la curva giace nella convex hull di questi; in pi¨ la proprietÓ di localitÓ garantisce che la curva, per t ∈ [tr,tr+1] sta anche nella convex hull dei punti [ti,ti+k], ovvero si ha la convex hull forte.
Linear precision (come conseguenza della strong convex hull) Se si hanno (k − 1) punti di controllo allineati dj+i = dj + αiv,r = 0,..,k − 1 l’equazione della curva diventa:
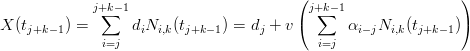 |
ovvero se almeno k − 1 punti sono allineati la curva tocca il segmento su cui giacciono i punti di controllo, e se almeno k lo sono la curva si schiaccia sul segmento stesso.
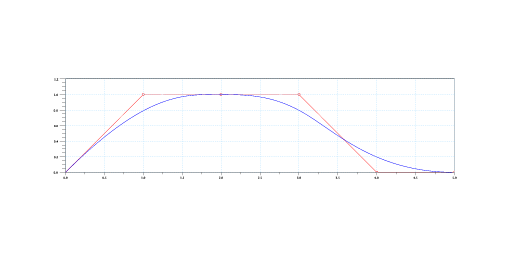 (a) k=4, 3 nodi allineati
(a) k=4, 3 nodi allineati
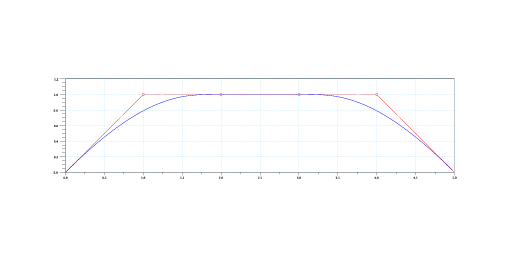 (b) k=4, 4 nodi allineati
(b) k=4, 4 nodi allineati
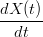 | = (k − 1) ∑
i=0nd
i![[ ]
-Ni,k−-1(t)-− Ni+1,k−1(t)
ti+k− 1 − ti ti+k − ti+1](tesi333x.png) | ||
= (k − 1) ∑
i=1n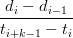 Ni,k−1(t) Ni,k−1(t) |
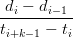 come di[1] (e ricorsivamente d
i[r] =
come di[1] (e ricorsivamente d
i[r] = ![[r−1] [r− 1]
di----−-di−1-
ti+k−1 − ti](tesi336x.png) ) si pu˛
generalizzare:
) si pu˛
generalizzare:
![r ∑n
d-X-(t) = (k − 1)...(k − r) d[r]Ni,k−1(t), t ∈ [tk−1,tn+1]
drt i=1 i](tesi337x.png) |
End point interpolation
In generale la proprietÓ di end point interpolation non vale per le B-SPLINE, ma la si pu˛
forzare.
Dato il vettore ausiliario t : t0,...,ti,...,ti+k−2,...,tk+μ+k, se i k-1 nodi ti,...,ti+k−2 coincidono si ha
che X(ti) = di−1. Quindi, forzando t0 = ... = tk−1 = τ0 e tk+μ+2 = ... = tk+μ+k = τn,
N0,k(t) = B0k−1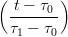 con t ∈ [τ0,τ1] e Nn,k(t) = Bk−1k−1
con t ∈ [τ0,τ1] e Nn,k(t) = Bk−1k−1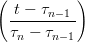 con t ∈ [τn−1,τn],
ovvero la proprietÓ Ŕ verificata.
con t ∈ [τn−1,τn],
ovvero la proprietÓ Ŕ verificata.
Derivata agli estrimi: raccordo Per disegnare una curva chiusa a derivate continue si deve imporre:
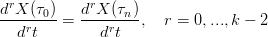 |
ovvero, per ogni r:
![∑n [r] ∑n [r]
(k − 1)...(k − r) di Ni,k− 1(τ0) = (k − 1)...(k − r) di Ni,k−1(τn)
i=1 i=1](tesi343x.png) |
Per le proprietÓ degli Ni,k:
![k− 2 n
(k − 1)...(k − r) ∑ d[r]N (τ ) = (k − 1)...(k − r) ∑ d[r]N (τ )
i=0 i i,k− 1 0 i=n−k+2 i i,k−1 n](tesi344x.png) |
da cui derivano direttamente le condizioni da imporre, ovvero:
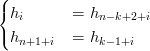 |
sempre per i = 0,...,k − 2
L’algoritmo di de Boor calcola i punti della curva in maniera analoga a quello di de Casteljau per le
curve di BÚzier.
Considerando t ∈ [tk−1,tn+1]
| X(t) | = ∑ i=0nd i(0)N i,k(t) | ||
= ∑
i=0nd
i(0)![[ ]
---t −-ti- -ti+k-−-t--
ti+k−1 − tiNi,k−1(t) + ti+k − ti+1 Ni+1,k−1(t)](tesi348x.png) | |||
= ∑
i=1n 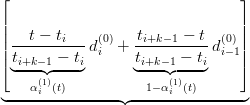 di(1)(t)Ni,k−1(t) di(1)(t)Ni,k−1(t) | |||
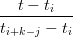 e di conseguenza di(j)(t) = α
i(j)(t)d
i(j−1)(t)+(1−α
i(j)(t))d
i−1(j−1)(t):
e di conseguenza di(j)(t) = α
i(j)(t)d
i(j−1)(t)+(1−α
i(j)(t))d
i−1(j−1)(t):
| X(t) | = ∑ i=jnd i(j)(t)N i,k−j(t) | ||
| = ∑ i=k−1nd i(k−1)(t)N i,1(t) |
Per t ∈ [tr,tr+1] si possono escludere dalla sommatoria iniziale i termini nulli:
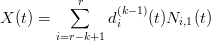 |
ed Ŕ possibile ottimizzare l’algoritmo.
Si vuole inserire un nodo t∗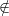 T tale che t∗ ∈ [t
r,tr+1] per creare il vettore T∗ = T ∪{t∗}, e definire
una curva su T∗ che sia identica a quella precedentemente definita su T. In particolare si definisce la
curva:
T tale che t∗ ∈ [t
r,tr+1] per creare il vettore T∗ = T ∪{t∗}, e definire
una curva su T∗ che sia identica a quella precedentemente definita su T. In particolare si definisce la
curva:
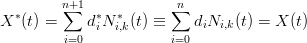 |
in cui:
| T∗ : t i∗ | = 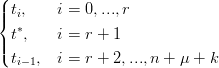 |
| αL,i | = 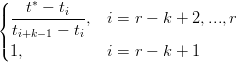 | ||
| αR,i | = 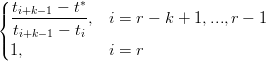 |
Ni,k∗(t) = 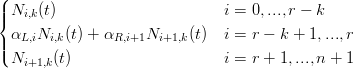 |
| X(t) | = ∑ i=0nd iNi,k(t) = ∑ i=0n+1d i∗N i,k∗(t) | ||
| = ∑ i=0r−kd i∗N i,k(t) + ∑ i=r−k+1rd i∗(α L,iNi,k(t) + αR,i+1Ni+1,k(t)) + ∑ i=r+1n+1d i∗N i+1,k(t) | |||
| = ∑ i=0r−k+1d iNi,k(t) + ∑ i=r−k+2r(d iαL,i + di−1αR,i)Ni,k(t) + ∑ i=r+1n+1d i−1Ni,k(t) |
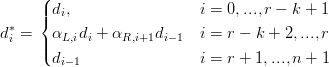 |
Le curve NURBS (Non Uniform Rational B-SPLINEs) sono un’estensione delle B-SPLINEs analoga
alla razionalizzazione delle curve di BÚzier.
La curva NURBS Ŕ definita come:
![∑n
βidiNi,k(t)
X (t) = i=0n----------, t ∈ [tk− 1,tn+1 ], T = {t0,...,tk− 1,...,tn+1,...,tn+k}
∑ β N (t)
i=0 i i,k](tesi361x.png) |
Per comoditÓ si indica con w(t) = ∑
i=0nβ
iNi,k(t) e di conseguenza con Ri,k(t) = 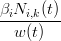 ; cosý
l’espressione della curva diventa:
; cosý
l’espressione della curva diventa:
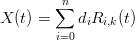 |
Le proprietÓ delle curve NURBS derivano direttamente da quelle delle B-SPLINEs, se βi > 0 ∀ i.
Per studiare l’influenza dei coefficienti si pu˛ calcolare cosa succede quando uno di questi cambia. Si definisce:
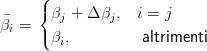 |
e di conseguenza:
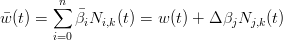 |
La nuova curva differisce dalla nuova di:
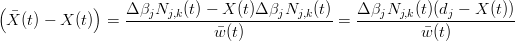 |
ovvero l’effetto Ŕ limitato dalla proprietÓ di localitÓ di Nj,k(t), ha verso (dj − X(t)) (cioŔ Ŕ in direzione del nodo interessato dal cambio di peso) e ha ampiezza Δβj.
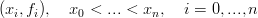 |
tali che† xi ∈ℝk e f i ∈Ed, il problema dell’interpolazione consiste nel trovare una curva f(t) (tipicamente una funzione polinomiale: f(t) ∈ Πn(t)) ed una parametrizzazione t = g(xi) per cui la funzione interpoli i dati forniti, ovvero:
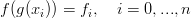 |
e scelte in modo che siano compatibili:
![(
{f : [a, b] → Ed
(
g : [x0,xn ] → [a, b]](tesi372x.png) |
Supponendo di vole usare la base di Lagrange† †Li,n(x) = ∏
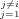 n
n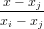 per definire un polinomio interpolante ai dati, si avrebbe un’espressione del tipo:
per definire un polinomio interpolante ai dati, si avrebbe un’espressione del tipo:
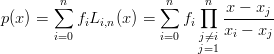 | (4.1) |
Da qui, per passare dal polinomio (4.1), strettamente legato agli xi, a una curva parametrica in t su un intervallo [a,b] arbitrario che sia interpolante gli stessi punti, si definisce:
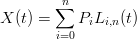 |
per la quale i punti di controllo Pi coincidono con i punti da interpolare fi, e i parametri ti
corrispondenti dipendono dalla parametrizzazione utilizzata.
Alcuni schemi di parametrizzazione sono:
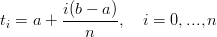 |
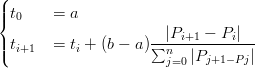 |
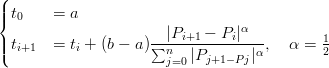 |
In generale questi stessi schemi di parametrizzazione si possono applicare nel dominio delle curve SPLINEs per segmentare il dominio della curva nei suoi sottodomini.
Si supponga di avere a disposizione i dati da interpolare in forma di triple:
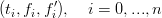 |
in cui fi rappresenta il valora da interpolare e fi′ la tangente alla curva nel punto di interpolazione; si cerca una funzione spline f(t) ∈ Πn che interpoli i dati in questo modo:
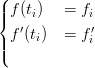 |
Ricapitolando, dati:
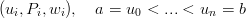 |
si pu˛ costruire una curva spline di terzo grado con continuitÓ C1 interpolante a partire dalla base di Bernstein. In particolare, si cerca una curva:
| X(u) | = Xi(u), u ∈ [ui,ui+1] | ||
| Xi(u) | = ∑
k=03b
k,iBk3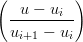 |
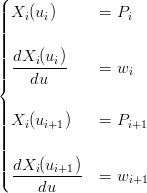 |
Dalle proprietÓ dei polinomi di Bernstein segue direttamente che per le condizioni agli estremi si devono imporre:
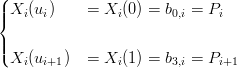 |
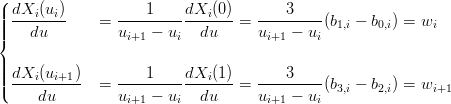 |
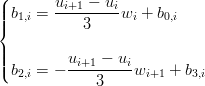 |
Se non si hanno a disposizione triplette di dati ma soltanto coppie (ui,fi), si possono definire degli schemi per approssimare i valori fi′ ed utilizzare comunque un approccio alla Hermite per l’interpolazione.
Schema FMILL Scegliendo di approssimare le derivate in questo modo:
| wi | = 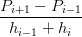 , i = 1,...,n , i = 1,...,n | ||
| w0 | = 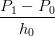 ,wn = ,wn = 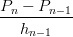 |
| Pi+1 | = F(ui+1) = F(ui) + hiF′(ui) +  hi2F′′(ξ) hi2F′′(ξ) | ||
| Pi−1 | = F(ui−1) = F(ui) + hi−1F′(ui) +  hi−12F′′(ζ) hi−12F′′(ζ) | ||
| Pi+1 − Pi−1 | = (hi−1 + hi)F′(ui) + O(h2) | ||
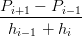 | = F′(ui) + O(h2) |
Tangenti di Bessel
L’idea alla base delle tangenti di Bessel Ŕ quella di considerare la derivata di un polinomio di
secondo grado interpolante tre punti consecutivi come terzo valore per il polinomio interpolante di
terzo grado.
Siano qi(u) curve polinomiali a tratti in Π2 tali che:
![q (u ) = P , j = i − 1,i,i + 1 u ∈ [u ,u ]
i j j i− 1 i+1](tesi396x.png) |
definite in questo modo:
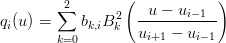 |
definendo t(u) = 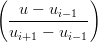 la precente pu˛ essere scritta:
la precente pu˛ essere scritta:
| qi(ui) = ∑ k=03b k,iBk2(t ui) | = Pi−1B02(t ui) + b1,1B12(t ui) + Pi+1B22(t ui) | ||
| = Pi−1(1 − tui)2 + 2b 1,itui(1 − tui) + Pi+1tui2 = defPi |
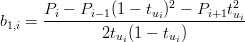 |
Mantenendo la notazione hi = ui+1 − ui, si ha che:
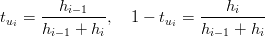 |
e si pu˛ riscrivere l’equazione precedente in questa forma:
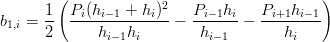 |
Ora che i polinomi qi sono definiti Ŕ possibile ricavare i valori wi per i punti di interpolazione in questo modo:
wi = 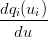 = = 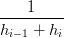 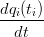 = = 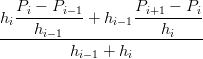 |
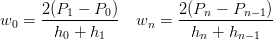 |
Questo schema fornisce un’approssimazione della derivata della curva, infatti:
| Pi | = F(ui) | ||
| Pi−1 | = Pi − F′(ui)hi−1 +  hi−12F′′(u
i) + O(hi−13) hi−12F′′(u
i) + O(hi−13) | ||
| Pi+1 | = Pi + F′(ui)hi +  hi2F′′(u
i) + O(hi3) hi2F′′(u
i) + O(hi3) | ||
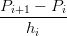 | = F′(ui) +  hiF′′(ui) + O(hi2) hiF′′(ui) + O(hi2) | ||
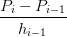 | = F′(ui) − hi−1F′′(ui) + O(hi−12) hi−1F′′(ui) + O(hi−12) | ||
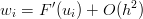 |
Dati:
 |
si vuole definire una spline C2 composta dalle curve:
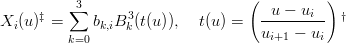 |
†per brevitÓ si pone ui+1 − ui = hi per le quali valgono le condizioni:
| Xi(ui) | = Xi−1(ui) = Pi | ||
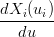 | = 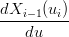 | ||
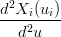 | = 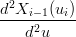 | ||
| b0,i | = Pi | ||
| b1,i | = Pi + 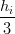 wi wi | ||
| b2,i | = Pi+1 −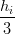 wi+1 wi+1 | ||
| b3,i | = Pi+1 | ||
Dalle condizioni di continuitÓ della derivata seconda 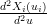 =
= 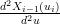 , segue che:
, segue che:
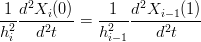 |
ovvero:
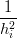 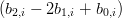 = = 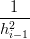 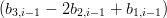 | ||
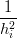 ![[( hi ) ( hi ) ]
Pi+1 − --wi+1 − 2 Pi + -- wi + (Pi)
3 3](tesi431x.png) | |||
= 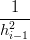 ![[ ( ) ( ) ]
hi− 1 hi−1
(Pi) − 2 Pi − -----wi + Pi−1 + ----wi−1
3 3](tesi433x.png) |
![[ P − P P − P ]
hiwi− 1 + 2 (hi− 1 + hi)wi + hi−1wi+1 = 3 hi−1-i+1-----i+ hi--i----i−1-
◟----------hi--◝◜-------hi−1---◞
Ti](tesi434x.png) |
I Tn sono tutti termini noti, e si ha un sistema di n−1† †considerando n intervalli equazioni in n + 1‡ ‡tutti i wi incognite, che pu˛ essere scritto nella forma:
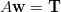 | (4.2) |
in cui:
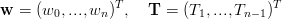 |
ed A Ŕ una matrice in M(n−1)×(n−1) ad elementi:
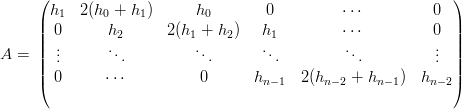 |
Rimangono da fissare i valori delle derivate agli estrimi w0 e wn. Alcune tra le scelte pi¨ comuni sono le seguenti:
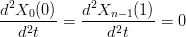 |
si ha, per i = 0:
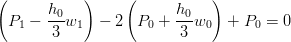 |
da cui:
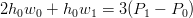 |
Per la derivata all’ultimo punto il ragionamento Ŕ analogo e si ha:
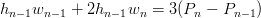 |
La matrice A ed il vettore T dell’equazione (4.2) possono essere allargati per comprendere i valori agli estremi:
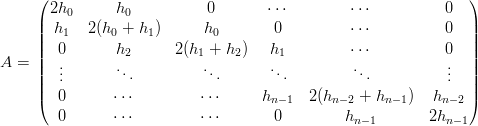 |
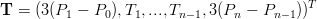 |
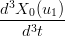 = = 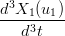 | →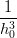 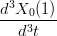 = = 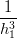 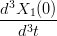 | ||
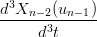 = = 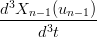 | →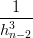 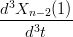 = = 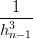 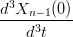 |
Svolgendo (la prima equazione, la seconda Ŕ analoga) si ottiene:
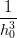 (b3,0 − 3b2,0 + 3b1,0 − b0,0) (b3,0 − 3b2,0 + 3b1,0 − b0,0) | = 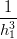 (b3,1 − 3b2,1 + 3b1,1 − b0,1) (b3,1 − 3b2,1 + 3b1,1 − b0,1) | ||
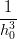 (2(P0 − P1) + h0w0 + h0w1) (2(P0 − P1) + h0w0 + h0w1) | = 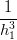 (2(P1 − P2) + h1w2 + h1w1) (2(P1 − P2) + h1w2 + h1w1) | ||
| h12w 0 + (h12 − h 02)w 1 − h02w 2 | = 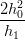 (P1 − P2) − (P1 − P2) −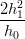 (P0 − P1) (P0 − P1) |
| β | = 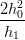 (P1 − P2) − (P1 − P2) −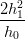 (P0 − P1) (P0 − P1) | ||
| γ | = 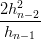 (Pn−1 − Pn) − (Pn−1 − Pn) −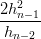 (Pn−2 − Pn−1) (Pn−2 − Pn−1) |
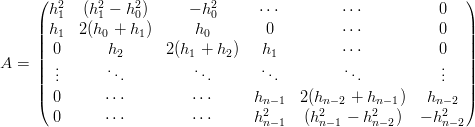 |
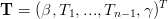 |
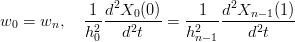 |
da cui:
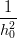 ![[( ) ( ) ]
P1 − h0w1 − 2 P0 + h0w0 + P0
3 3](tesi474x.png) | |||
= 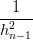 ![[ ( h ) ( h ) ]
Pn − 2 Pn + --n−1wn + Pn −1 − -n−-1wn−1
3 3](tesi476x.png) |
h0wn−1 + 2(h0 + hn−1)w0 + hn−1w1 = 3![[ ]
P1-−-P0- Pn-−-Pn-−1
hn−1 h0 + h0 hn−1](tesi477x.png) |
![[ P − P P − P ]
β = 3 hn −1-1-----0+ h0 -n-----n−1
h0 hn−1](tesi478x.png) |
la matrice A e i vettori T,w dell’equazione (4.2) diventano:
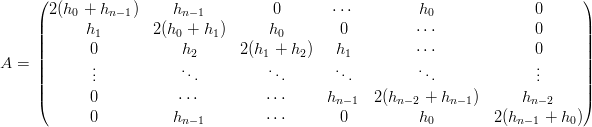 |
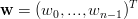 |
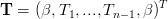 |
in cui la condizione w0 = wn Ŕ imposta implicitamente nella prima e ultima riga della matrice.
Sia s(u) una spline cubica C2 tale che:
 |
e y(u) una funzione qualsiasi C2 a sua volta tale che:
 |
La quantitÓ:
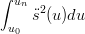 |
Ŕ una possibile misura del grado di oscillazione della curva.
Si dimostra che vale la relazione:
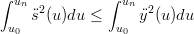 |
Infatti:
| ř(u) | = (ř(u) −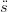 (u)) + (u)) + 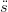 (u) (u) | ||
| ř2(u) | = 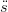 2(u) + (ř(u) − 2(u) + (ř(u) −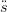 (u))2 + 2 (u))2 + 2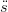 (u)(ř(u) − (u)(ř(u) −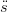 (u)) (u)) | ||
| ∫ u0un ř2(u)du | = ∫
u0un
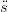 2(u)du + ∫
u0un
(ř(u) − 2(u)du + ∫
u0un
(ř(u) −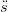 (u))2du + 2 ∫
u0un (u))2du + 2 ∫
u0un
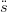 (u)(ř(u) − (u)(ř(u) −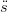 (u))du (u))du |
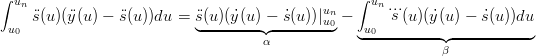 |
in cui α = 0 ed in quanto ... s(u) Ŕ costante a tratti, β pu˛ essere trasformato nella somma:
![n−1
∑ si[y(u) − s(u)]ui+1
i=0 ui](tesi502x.png) |
che a sua volta Ŕ nulla perchŔ valgono le condizioni y(ui) = s(ui).
Un’altra misura della stessa quantitÓ pu˛ essere ottenuta dalla curvatura, considerando come
parametro la lunghezza dell’arco:
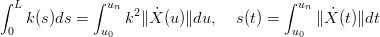 |
Rappresentando la funzione vettorialmente:
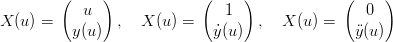 |
la curvatura assume espressione:
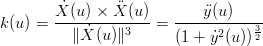 |
da cui:
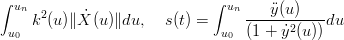 |
Data una spline in forma di BÚzier:
| X(u) = Xi(u), u ∈ [ui,ui+1] | ||
Xi(t) = ∑
i=03b
k,iBk3(t), t = 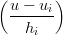 |
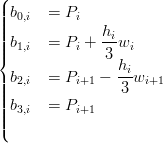 |
Imponendo le condizioni di raccordo, considerando ω1,i = 1 si ottiene:
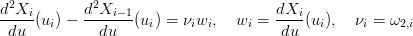 |
Le condizioni di raccordo permettono di scrivere infine le equazioni:
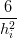 ![[ ]
(P − hiw ) − 2(P + hiw ) + P
i+1 3 i+1 i 3 i i](tesi511x.png) − − | |||
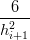 ![[ ]
Pi − 2(Pi − hi−-1wi) + (Pi− 1 + hi−-1wi−1)
3 3](tesi513x.png) − νiwi = 0 − νiwi = 0 |
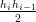 si ottiene infine:
si ottiene infine:
![[ ] [ ]
νi Pi+1 −-Pi- Pi-−-Pi−1-
hiwi + 2(hi−1 + hi) + 2 hihi−1 wi + hi− 1wi+1 = 3 hi− 1 hi + hi hi− 1](tesi515x.png) |
ovvero si ottiene un sistema analogo a quello delle spline C2 con un termine in pi¨ sulla diagonale:
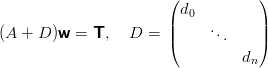 |
in cui d0,dn sono assegnati e di = 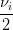 hi−1hi.
hi−1hi.
Per ottenre una spline chiusa, supponendo di avere il primo punto uguale al primo (P0 = Pn) si ha
invece un sistema in n incognite in cui le prime e le ultime equazioni di A sono analoghe a quelle per
la spline periodica precedentemente ricavate, ovvero del tipo:
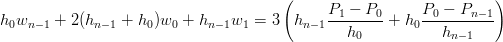 |
e inoltre
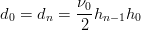 |
╚ interessante osservare cosa succede per νmin →∞. Innanzitutto serve calcolare:
| (A + D)w | = T | ||
| (AD−1 + I)(Dw) | = T | ||
(I + E)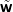 | = T, E = AD, 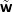 = Dw = Dw |
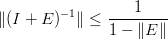 |
si ha che:
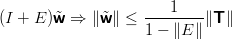 |
ovvero se D →∞, w → 0.
Una superficie, in maniera analoga ad una curva, pu˛ essere rappresentata in modo parametrico come l’immagine di una funzione continua e iniettiva di due variabili reali X : (A ∈ℝ2) →E3 tale che:
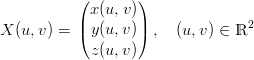 |
Definizione 5.1 (Superficie parametrica regolare).
La superficie parametrica si dice regolare se valgono le condizioni:
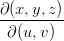 =
= ![[x y z ]
u u u
xv yv zv](tesi528x.png) abbia rango 2, ovvero le derivate non
si annullano mai entrambe in uno stesso punto
abbia rango 2, ovvero le derivate non
si annullano mai entrambe in uno stesso punto
Definizione 5.2 (Vettori associati alla superficie: tangenti e normale). Per comoditÓ nello studio delle proprietÓ della superficie si definiscono i vettori:
Xu = 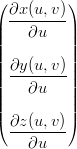 , Xv = , Xv = 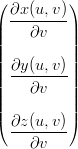 | ||
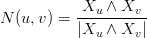 |
Osservazione 5.1 (Caratteristiche dei vettori Xu,Xv,N(u,v)). Se la superficie Ŕ regolare si ha che i vettori Xu e Xv sono linearmente indipendenti e non paralleli, ovvero Xu ∧ Xv≠0; di conseguenza anche N(u,v)≠0 ∀(u,v) ∈ A.
Sfera La sfera† †centrata nell’origine degli assi Ŕ definibile come il luogo geometrico dei punti equidistanti dall’origine:
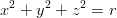 |
Una possibile parametrizzazione per i punti della superficie sferica si pu˛ dare a partire dai parametri
u ∈ [−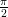 ,
,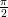 ] e v ∈ [0, 2π]:
] e v ∈ [0, 2π]:
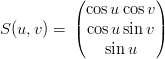 |
I vettori tangenti alla superficie sono quindi:
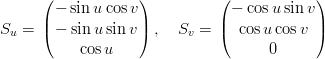 |
Cono Un cono Ŕ lo spazio geometrico dei punti che soddisfano l’equazione:
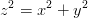 |
Una parametrizzazione in due parametri u ∈ [−L,L], v ∈ [0, 2π] Ŕ:
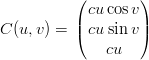 |
I vettori tangenti sono, di conseguenza:
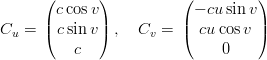 |
Si definiscono due nuovi parametri in funzione di quelli vecchi:
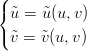 |
Data la matrice:
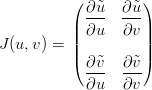 |
la riparametrizzazione si definisce ammissibile se det J(u,v)≠0. In particolare si ha che:
Xu ∧ Xv = 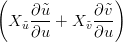 ∧ ∧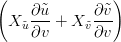 = = 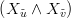 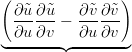 det J(u,v) det J(u,v) |
Una superficie di rivoluzione Ŕ una superficie ottenuta ruotando una curva (chiamata curva generatrice
o profilo) intorno ad un asse (detto asse di rotazione). La circonferenza ottenuta interesecando
un piano perpendicolare all’asse di rotazione con la superficie Ŕ detta parallelo, la curva
ottenuta intersecando la superficie con un piano passate per l’asse di rotazione Ŕ detta
meridiano.
In generale una superficie di rotazione Ŕ rappresentabile in modo parametrico. Sia una curva C
definita parametricamente come:
![(
{ C (u)
C (u ) = x , u ∈ [a,b]
( Cy(u)](tesi554x.png) |
La curva C pu˛ essere fatta ruotare intorno all’asse z definendo la superficie:
![(
||{ Cx (u )cos(v)
X (u,v) = Cy (u )sin (v) , v ∈ [0,2π]
||(
Cx (u )](tesi555x.png) |
Una superficie rigata Ŕ una superficie ottenuta da un’unione di rette.
Definizione 5.3 (Superficie rigata). Una superficie S si dice rigata se esiste una famiglia di
rette rα tale che S Ŕ l’unione delle rette di tale famiglia: S = ∪αrα.† †Una definizione equivalente Ŕ che S Ŕ rigata se per ogni punto di S passa una retta rs che sia tutta
contenuta in essa.
Date due curve C0(u),C1(u) e due parametri u ∈ [a,b],v ∈ [0, 1] una superficie rigata pu˛ essere difinita parametricamente come:
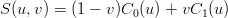 |
ovvero si sfrutta l’esistenza di una corrispondenza univoca tra i punti di C0 e quelli di C1.
Se C0 e C1 sono segmenti, ovvero sono parametrizzabili come:
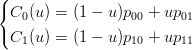 |
la superficie rigata S pu˛ essere scritta come:
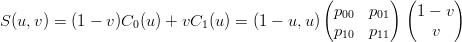 |
Definizione 5.4 (Tensor product). Date due funzioni monovariate S1,S2 tali che:
| S1 =< f0,...,fn >, | f0,...,fn funzioni monovariate in u ∈ [a,b] | ||
| S2 =< g0,...,gm >, | g0,...,gm funzioni monovariate in v ∈ [c,d] |
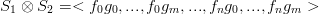 |
S1 ⊗ S2 Ŕ pertanto una funzione bivariata, e vale:
![∑n m∑
S (u, v) ∈ S ⇔ S(u,v) = bijfi(u)gj(v), (u,v) ∈ [a, b] × [c,d]
i=0j=0](tesi562x.png) |
Il tensor product pu˛ quindi essere utilizzato per definire superfici, considerando funzioni del tipo:
![n m
∑ ∑
X (u,v) = bijfi(u)gj(v), (u,v) ∈ [a, b] × [c,d]
i=0j=0](tesi563x.png) |
La patch di BÚzier Ŕ definita a partire dalla base omonima nel modo seguente:
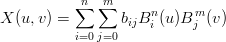 |
Curve di contorno La superficie Ŕ delimitata da quattro curve di contorno† †boundary :
![( ∑m m
|||| u = 0,v ∈ [0,1], X (0,v) = ∑ j=0 b0jB j (v )
|||| u = 1,v ∈ [0,1], X (1,v) = mj=0 b1jBmj (v )
{ ∑n n
|| v = 0,u ∈ [0,1], X (u,0 ) = ∑ i=0 bi0B i (u)
|||| v = 1,u ∈ [0,1], X (u,1 ) = ni=0 bi1Bni (u)
||(](tesi565x.png) |
Posizione negli angoli Negli angoli la supericie Ŕ parallela al piano individuato dai punti di controllo. Infatti, considerando le derivate prime parziali della superficie lungo le due direzioni negli angoli, si ha:
| Ẋu(0, 0) | = nΔ(1,0)b 0,0 = n(b1,0 − b0,0) | ||
| Ẋu(1, 0) | = n∑ i=0n−1Δ(1,0)b i,0Bin−1(1) = nΔ(1,0)b n−1,0 = n(bn,0 − bn−1,0) | ||
| Ẋv(0, 0) | = nΔ(0,1)b 0,0 = m(b0,1 − b0,0) | ||
| Ẋv(0, 1) | = m∑ j=0m−1Δ(0,1)b 0,jBjm−1(1) = mΔ(0,1)b 0,m−1 = m(b0,m − b0,m−1) |
Altre proprietÓ In quanto somme di polinomi di Bernstein valgono le seguenti proprietÓ, dimostrabili in modo analogo a quanto giÓ mostrato in modo esplicito per le curve di BÚzier:
Forma compatta La superficie X(u,v) pu˛ essere espressa in forma compatta come:
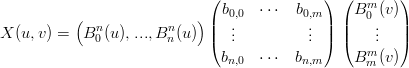 |
L’algoritmo di de Casteljau per le superfici funziona in maniera del tutto analoga a quello descritto
precedentemente per le curve.
Dati bij00 = b ij come punti iniziali per l’algoritmo (i = 0,..,n; j = 0,...,m), si definisce il passo dell’algoritmo unidirezionale (nelle due direzioni, rispettivamente) in questo modo:
| bijk0(u) | = (1 − u)b ijk−1,0 + ub i+1,jk−1,0, i = 0,...,n − k | ||
| bij0k(v) | = (1 − v)b ij0,k−1 + vb i,j+10,k−1, j = 0,...,m − k |
Svolgendo contemporaneamente nelle due direzioni si ha:
| bijkl(u,v) | = (1 − v)b ijk,l−1 + vb i,j+1k,l−1 | ||
= (1 − v)![[ k−1,l−1 k−1,l−1]
(1 − u)bij + ubi+1,j](tesi567x.png) + v + v![[ k− 1,l− 1 k− 1,l− 1]
(1 − u )bi,j+1 + ubi+1,j+1](tesi568x.png) |
bijkl(u,v) =  (1 − u),u (1 − u),u 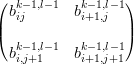 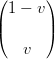 , i = 0,...,n − k; j = 0,...,m − l , i = 0,...,n − k; j = 0,...,m − l |
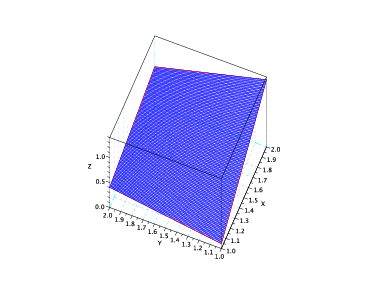
L’algoritmo di degree elevation consente di elevare il grado della patch di BÚzier lungo una delle due direzioni aggiungendo una riga di punti di controllo e modificando quelli esistenti in modo opportuno. In particolare, data la superficie:
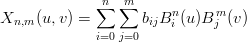 |
si vuole aumentarne il grado lungo una direzione, ovvero ottenere:
| Xn+1,m(u,v) | = ∑ i=0n+1 ∑ j=0mc ijBin+1(u)B jm(v) | ||
| oppure | |||
| Xn,m+1(u,v) | = ∑ i=0n ∑ j=0m+1d ijBin(u)B jm+1(v) | ||
| Xn,m(u,v) | = ∑ i=0n ∑ j=0mb ijBin(u)B jm(v) | ||
= Xn+1,m(u,v) = ∑
i=0n+1 ∑
j=0mc
ijBin+1(u)B
jm(v) = ∑
j=0m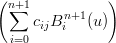 Bjm(v) Bjm(v) |
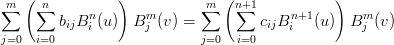 |
che implica:
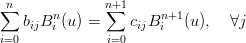 |
I nuovi punti di controllo sono pertanto:
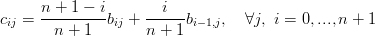 |
Gli stessi ragionamenti si applicano in modo perfettamente analogo anche all’altro caso.
In generale si preferisce aumentare il grado contemporaneamente in entrambe le direzioni. Applicando lo stesso ragionamento anche nell’altra direzione si ottiene:
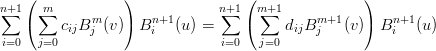 |
da cui, come prima:
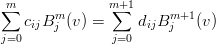 |
che implica:
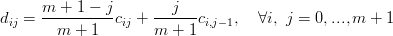 |
Esplicitando i cij si ottiene:
| dij | = 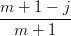 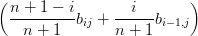 + + 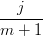 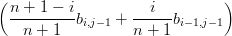 | ||
= 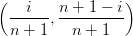 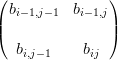 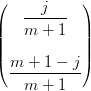 |
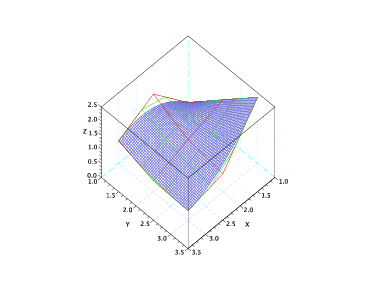
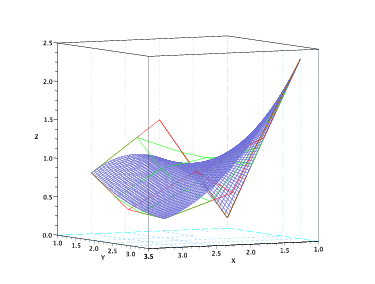
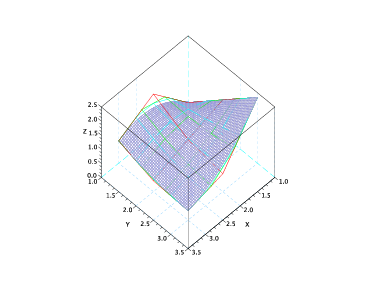
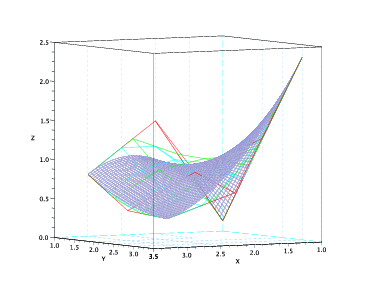
L’algoritmo di subdivision lungo una delle due direzioni Ŕ analogo a quello per le curve. Data la superficie:
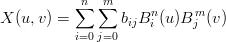 |
la si vuole suddividere in due superfici lungo una delle due direzioni:
![(
||| ∑n ∑m n m ^ t
{XL (τ,v ) = i=0 j=0 cijB i (τ)B j (v) = X (t,v), t ∈ [0,t], τ = ^t ∈ [0,1 ]
|| ∑n ∑m t − ^t
|(XR (τ, v) = i=0 j=0 dijBni (τ )Bmj (v) = X (t,v ), t ∈ [^t,1], τ =----^ ∈ [0,1]
1 − t](tesi597x.png) |
oppure lungo l’altra:
![(
|| ∑n ∑m n m t
|{ XL (u,τ ) = i=0 j=0 cijB i (u)B j (τ ) = X (u, t), t ∈ [0,^t], τ = ^ ∈ [0, 1]
| ∑ ∑ tt − ^t
||( XR (u,τ ) = ni=0 mj=0 dijBni (u )Bmj (τ) = X (u,t), t ∈ [^t,1 ], τ =---- ∈ [0,1]
1 − ^t](tesi598x.png) |
In entrambi i casi, in modo analogo al caso bidimensionale i coefficienti si ottengono a partire da quelli dell’algoritmo di de Casteljau:
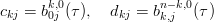 |
per la direzione u e:
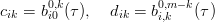 |
lungo v.
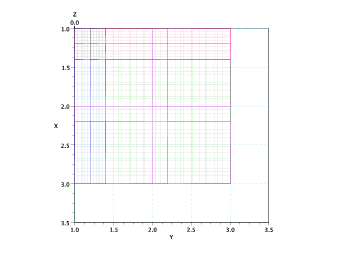
Una superficie tensor-product di BÚzier, come definita in precedenza, Ŕ una funzione del tipo:
![∑n ∑m n m
X (u,v) = bijBi (u )Bj (v), (u,v) ∈ [0,1] × [0,1]
i=0j=0](tesi607x.png) |
In questo caso, definiti:
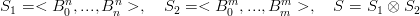 |
si ha che si sta lavorando su uno spazio di dimensione:
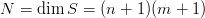 |
Il problema dell’interpolazione di superfici quindi Ŕ completamente determinanto se si hanno a disposizione N campionamenti della superficie da interpolare; i dati del problema sono rappresentabili come:
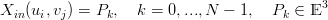 |
Se si hanno a disposizione campionamenti sparsi della superficie che si vuole interpolare:
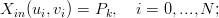 |
si va a risolvere il sistema:
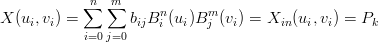 |
il quale pu˛ essere scritto nella forma:
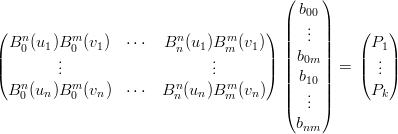 |
Se i campionamenti sono distribuiti su una griglia rettangolare:
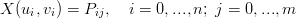 |
si vuole risolvere, come prima, il sistema:
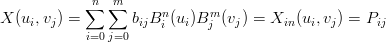 |
Per ogni coppia di punti si ha:
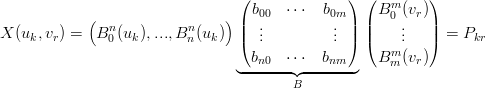 |
Definita la matrice dei punti noti:
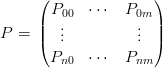 |
e le matrici:
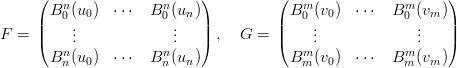 |
il problema pu˛ essere rappresentato in forma matriciale come
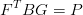 |
L’idea alla base delle patch triangolari Ŕ quella di usare una combinazioni baricentrica di coordinate
come parametri per muoversi su una superficie. In particolare in questo caso si considera come
dominio un triangolo non degenere T,di vertici 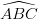 ; i punti dell’area sono rappresentabili come
combinazione baricentrica dei vertici:
; i punti dell’area sono rappresentabili come
combinazione baricentrica dei vertici:
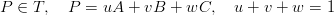 |
e la superficie come una funzione:
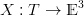 |
Le coordinate baricentriche descritte sopra sono in relazione biunivoca con quelle cartesiane. Si ha:
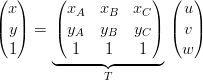 |
AffinchŔ la relazione sia biunivoca (ovvero il sistema ha soluzione unica) se e solo se la matrice T Ŕ
non singolare, ovvero il triangolo 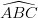 non Ŕ degenere.
non Ŕ degenere.
I polinomi di Bernstein possono essere generalizzati alle coordinate baricentriche. Per comoditÓ si utilizza la seguente notazione:
Definizione 5.5 (polinomio di Bernstein generalizzato). Si definisce polinomio di Bernstein generalizzato il polinomio:
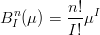 |
Tale polinomio Ŕ bivariato e di grado n, infatti μI = uivjwk e i + j + k = n.
Fissare |I| = n riduce il numero di indici distinti a (n + 1)(n + 2)∕2.
Non negativitÓ Tutti i fattori sono positivi o nulli, e la propritÓ Ŕ banalmente soddisfatta.
Partizione dell’unitÓ Vale che:
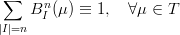 |
Dimostrazione. si ha infatti che:
| 1 = 1n | = (u + v + w)n = (u + (v + w))n | ||
= ∑
i=0n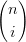 ui(v + w)n−i ui(v + w)n−i | |||
= ∑
i=0n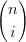 ui ∑
j=0n−i ui ∑
j=0n−i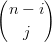 vjw vjw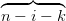 k k
| |||
= ∑
i=0n ∑
j=0n−i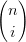 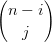 uivjwk uivjwk | |||
= ∑
i=0n ∑
j=0n−i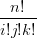 uivjwk uivjwk | |||
= ∑
|I|=n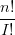 μI μI | |||
| = BIn(μ) |
Linear Precision Si pu˛ dimostrare che vale:
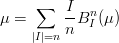 |
la dimostrazione Ŕ componente per componente e si riconduce direttamente alla proprietÓ analoga giÓ dimostrata nel caso monovariato.
Ora Ŕ possibile dare una definizione pi¨ rigorosa delle patch triangolari di BÚzier.
Definizione 5.6 (Patch triangolare di BÚzier). Dato un dominio triangolare T, una patch triangolare di BÚzeire di grado n Ŕ una funzione X : T →E3 del tipo:
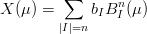 |
in cui bI ∈E3 sono chiamati punti di controllo.
Comportamento ai bordi Lungo uno dei bordi (ovvero quando uno dei tre parametri in μ Ŕ nullo si ha:
X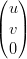 | = ∑
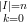 bIBIn bIBIn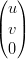 | ||
= ∑
i=0nb
(i,n−i,0)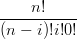 uivn−iw0 uivn−iw0 | |||
= ∑
i=0nb
(i,n−i,0) 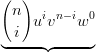 Bin(n), v=1−u Bin(n), v=1−u |
Controllo pseudolocale Spostando un punto di controllo:
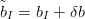 |
si ha:
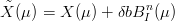 |
ovvero come nel caso delle curve di BÚzier la modifica di un punto di controllo ha effetti su tutta la curva, in maniera proporzionale al valore del polinomio di Bernstein corrispondente.
Ai vertici del triangolo si ha:
X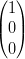 | = ∑
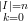 bIBIn ∑
i=0nb
(i,0,0) bIBIn ∑
i=0nb
(i,0,0)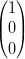 = ∑ = ∑
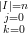 bIBIn bIBIn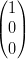 | ||
= ∑
i=nnb
(i,0,0)B(i,0,0)n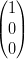 | |||
= b(n,0,0)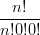 1nv0w0 = b
(n,0,0) 1nv0w0 = b
(n,0,0) |
I polinomi di BÚrnstein generalizzati posso essere espressi in forma ricorsiva:
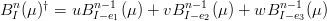 | (5.1) |
†in cui con e1,e2,e3 si indicano i versori unitari lungo le direzioni u,v,w Infatti:
| BI−e1n−1(μ) | = 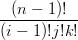 ui−1vjwk ui−1vjwk | ||
| BI−e2n−1(μ) | = 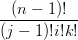 uivj−1wk uivj−1wk | ||
| BI−e3n−1(μ) | = 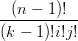 uivjwk−1 uivjwk−1 |
![[ 1 1 1] (n − 1)! n!
---+ ---+ -- ----------------------uivjwk = -----uivjwk =def BnI(μ)
jk ik ij (i − 1 )!(j − 1)!(k − 1)! i!j!k!](tesi655x.png) |
Come nel caso delle patch quadrate di BÚzeir, l’algoritmo di de Casteljau si definisce a partire dalla
definizione ricorsiva del polinomi di Bernstein.
Si definiscono i punti di controllo al passo zeresimo:
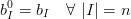 |
La superficie Ŕ definita dai punti:
| X(μ) | = ∑ |I|=nbI0B In(μ) | ||
= ∑
|I|=nbI0![[uBn −1(μ ) + vBn −1 (μ) + wBn −1 (μ)]
I−e1 I−e2 I−e3](tesi657x.png) | |||
| = ∑ |J|=n−1(ubJ+e10 + vb J+e20 + wb J+e30)B Jn−1(μ) |
e definendo:
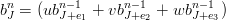 |
in generale la superficie pu˛ essere rappresentata come:
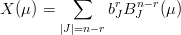 |
i cui singoli punti sono quindi in:
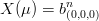 |
Data la superficie:
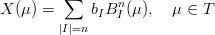 |
la si vuole rappresentare con una patch di bezier di grado pi¨ elevato:
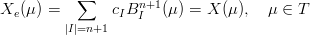 |
In quanto u + v + w = 1 si pu˛ scrivere:
| X(μ) | = ∑ |I|=nbIBIn(μ) = (u + v + w) ∑ |I|=nbIBIn(μ) | ||
= ∑
|I|=nbI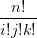 ui+1vjwk + ∑
|I|=nbI ui+1vjwk + ∑
|I|=nbI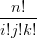 uivj+1wk + ∑
|I|=nbI uivj+1wk + ∑
|I|=nbI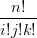 uivjwk+1 uivjwk+1 | |||
= †∑
|I|=nbI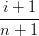 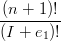 UI+e1
+ ∑
|I|=nbI UI+e1
+ ∑
|I|=nbI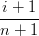 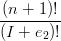 UI+e2
+ ∑
|I|=nbI UI+e2
+ ∑
|I|=nbI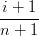 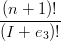 UI+e3 UI+e3
| |||
= ‡∑
|J|=n+1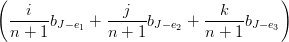 BJn+1(μ) BJn+1(μ) | |||
| = ∑ |J|=n+1cIBJn+1(μ)asd |
†Chiamando uivjwk = UI
‡Considerato che 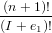 UI+e1 = BI+e
1n+1 e cosý via
UI+e1 = BI+e
1n+1 e cosý via
ovvero i coefficienti cI possono essere ricavati direttamente:
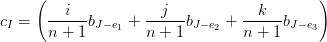 |
All’inizio di ogni script di esempio, tutti denominati esempi˙*.sci, c’Ŕ una lista di selettori per selezionare quali figure si vogliono prodotte.