†La matrice jacobiana è la matrice di tutte le derivate parziali prime di una funzione che ha dominio e codominio in uno spazio euclideo. Una funzione F : ℝn → ℝm è descritta in modo parametrico attraverso le sue componenti: (F1(x ,...,x ) 1 n,...,Fm(x ,...,x ) 1 n)T e la relativa matrice Jacobiana è definita come:

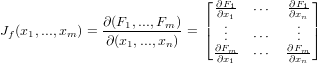⌊∂F1 ⋅⋅⋅ ∂F1⌋ ∂(F1,...,Fm-) | ∂x1. ∂x.n| Jf(x1,...,xm) = ∂(x1,...,xn ) = ⌈ .. ⋅⋅⋅ .. ⌉ ∂F∂xm1- ⋅⋅⋅ ∂∂Fxmn-