∈ℝ approssimazione del risultato esatto x ∈ℝ. É possibile definire la grandezza errore
assoluto come:
∈ℝ approssimazione del risultato esatto x ∈ℝ. É possibile definire la grandezza errore
assoluto come:
Si supponga di avere a disposizione un metodo numerico che dia come risultato un numero
 ∈ℝ approssimazione del risultato esatto x ∈ℝ. É possibile definire la grandezza errore
assoluto come:
∈ℝ approssimazione del risultato esatto x ∈ℝ. É possibile definire la grandezza errore
assoluto come:
△x =  − x
− x
o in altra forma:
 = x + △x.
= x + △x.
Questa grandezza, benché fornisca un’indicazione precisa del valore dell’errore commesso dal metodo matematico preso in esame, non permette di valutare quanta influenza abbia l’errore sul risultato ottenuto. Ad esempio, un errore assoluto △x = O(10−5) potrebbe avere un peso accettabile se il nostro risultato corretto x fosse dell’ordine di grandezza O(1) o superiore, ma non si avrebbe un risultato valutabile se x fosse anch’esso O(10−5).
Volendo conoscere quanto un errore influenzi il risultato quando x≠0, si definisce l’errore relativo:
εx ≡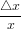 =
= 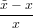
da cui:
 = x(1 + εx), e quindi
= x(1 + εx), e quindi  = 1 + εx
= 1 + εx
ovvero l’errore relativo deve essere comparato a 1: un errore relativo vicino a zero indicherà che il risultato approssimato è molto vicino al risultato esatto,mentre un errore relativo uguale a 1 indicherà la totale perdita di informazione.
Sia x = π ≃ 3.1415 =  . L’errore relativo è quindi: εx =
. L’errore relativo è quindi: εx = 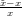 ≃
≃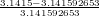 = −0.000029492.
Notiamo che la formula: −log10(εx) restituisce all’incirca il numero di cifre significative
corrette all’interno di
= −0.000029492.
Notiamo che la formula: −log10(εx) restituisce all’incirca il numero di cifre significative
corrette all’interno di  : in questo caso il risultato del calcolo è 4.53, che è abbastanza vicino
alla realtà di 5 cifre significative corrette.
: in questo caso il risultato del calcolo è 4.53, che è abbastanza vicino
alla realtà di 5 cifre significative corrette.
I calcolatori elettronici non sono in grado di lavorare su un insieme numerico continuo, ma sono limitati a operare su un insieme numerico finito e discreto. In generale, però, i problemi matematici sono naturalmente pensati su un insieme continuo, ed è necessario sostituirli con opportuni problemi discreti che il calcolatore è in grado di gestire. Ad esempio, si supponga di voler calcolare un’approssimazione della derivata prima di una funzione derivabile f in un punto assegnato x0:
f′(x0) ≃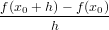 con h > 0.
con h > 0.
L’incremento h, per quanto piccolo, è una quantità finita.
Consideriamo l’espansione in serie di Taylor con resto al secondo ordine:
f(x0 + h) = f(x0) + hf′(x0) + 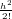 f′′(ψ) con ψ ∈ (x0,x0 + h)
f′′(ψ) con ψ ∈ (x0,x0 + h)
sostituendo si ha:
f′(x0) ≃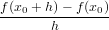 = f′(x0) +
= f′(x0) +  f′′(ψ)
f′′(ψ)
dove il termine  f′′(ψ) quantifica l’errore di discretizzazione, che in questo caso è un
O(h).
f′′(ψ) quantifica l’errore di discretizzazione, che in questo caso è un
O(h).
Consideriamo invece la formula:
f′(x0) = 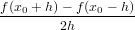 con h > 0
con h > 0
e lo sviluppo in serie di Taylor di f(x) di punto inziale x0 con resto al terzo ordine si ottiene:
f′(x0) =
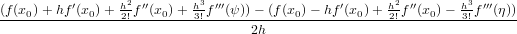 con ψ ∈ (x0,x0 + h) e η ∈ (x0 − h,x0)
con ψ ∈ (x0,x0 + h) e η ∈ (x0 − h,x0)
ovvero:
f′(x0) = f′(x0) + 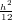 (f′′′(ψ) − f′′′(η))
(f′′′(ψ) − f′′′(η))
In questo caso l’errore commesso è O(h2), minore rispetto al caso precedente.
Questo esempio mostra come, approssimando un problema continuo a un problema discreto
in due modi diversi, vi possa essere una grossa differenza nell’errore di discretizzazione
commesso.
Spesso per risolvere un problema è possibile definire un metodo numerico di tipo iterativo che approssimi il risultato esatto, qui indicato con , attraverso una successione di risultati intermedi {xn}, ricavabili mediante la funzione di iterazione del metodo:
xn+1 = Φ(xn), n = 0,1,2...,
Ovviamente, affinché il calcolo iterativo possa avere inizio, è necessario definire un x0
approssimazione iniziale su cui eseguire il metodo la prima volta.
Condizione minimale che rende il metodo iterativo utile è che sia verificata la condizione di
consistenza: Φ() = .
Un metodo iterativo si potrà dire convergente se:
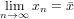 |
tuttavia, il risultato corretto è disponibile solo dopo infinite iterazioni. Ovviamente al di fuori del mondo matematico si sarà costretti ad eseguire un numero finito di iterazioni, rendendo quindi necessario definire un opportuno criterio di arresto che all’n-esimo ciclo arresti la successione e determini l’errore:
△x = xn −
detto errore assoluto di convergenza del metodo Φ(xn).
Il metodo iterativo appena descritto, convergente a , deve verificare la condizione di
consistenza; ovvero la soluzione cercata deve essere un punto fisso per la funzione di
iterazione che definisce il metodo.
Dimostrazione:
Supponiamo che non valga la condizione di consistenza, ovvero Φ()≠. Allora se all’n-esimo
passo dell’iterazione xn = , xn+1≠ e non sarebbe vero che limn→∞xn = , ovvero la
funzione non sarebbe convergente e non sarebbe possibile arrivare a un risultato nemmeno
dopo infinite iterazioni.
Il metodo iterativo
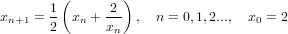 |
definisce un metodo numerico convergente per calcolare 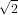 .
.
Dimostrazione: 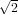 è un punto fisso per la funzione, infatti:
è un punto fisso per la funzione, infatti:
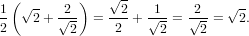 |
e quindi vale la condizione di consistenza.
La funzione converge a 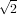 e a ogni passo dell’iterazione la distanza dal valore corretto
diminuisce, ovvero:
e a ogni passo dell’iterazione la distanza dal valore corretto
diminuisce, ovvero:
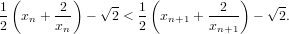 |
Dal momento che consideriamo x0 = 2, la funzione si avvicina a 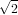 per valori positivi.
Quindi:
per valori positivi.
Quindi:
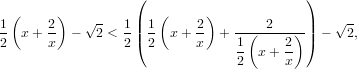 |
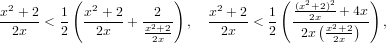 |
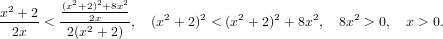 |
Ovvero per ogni x > 0 punto di innesco della sequenza, questa converge a 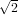 .
Cvd.
.
Cvd.
Il metodo iterativo:
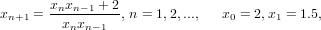 |
fornisce una successione di approssimazioni convergente a 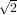 .
.
Ecco un esempio di successione, arrestata a un errore di convergenza ≈ 10−12, considerando
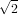 = 1.414213562374:
= 1.414213562374:
| n | xn | εconv |
| 0 | 2 | 4.1 ∗ 10−1 |
| 1 | 1.5 | 6.0 ∗ 10−2 |
| 2 | 1.42 | 4.1 ∗ 10−3 |
| 3 | 1.4137 | 3.6 ∗ 10−4 |
| 4 | 1.41423 | 1.2 ∗ 10−5 |
| 5 | 1.41421358 | 1.2 ∗ 10−8 |
| 6 | 1.41421356237339 | 4.3 ∗ 10−13 |
Gli errori di round-off si verificano quando si cerca di rappresentare dei numeri che contengano intrinsecamente una quantità infinita di informazione (come ad esempio i numeri irrazionali) all’interno di una memoria dalle dimensioni finite che quindi obbliga a utilizzare un’approssimazione di questi.
Un numero intero è rappresentato, all’interno di un calcolatore, come una stringa del tipo:
α0α1....αn
per cui, assegnata una base b ∈ℕ:
α0 ∈{+,−}, αi ∈{0,1,...,b − 1}, i = 1,....,N.
A questa stringa viene fatto corrispondere il numero intero:
n = 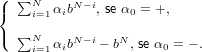
In particolare nel caso di α0 positivo si ha che:
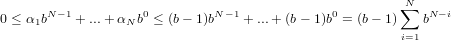 |
ovvero il massimo numero positivo rappresentabile è:
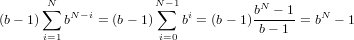 |
e quindi l’intervallo di numeri positivi rappresentabile è: [0,bN − 1]
mentre quello di numeri negativi è: [−bN,−1].
Mediante questo sistema è possibile rappresentare senza errore tutti gli interi nell’insieme
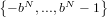 .
.
Un numero reale è rappresentato come una stringa del tipo:
α0α1...αmβ1β2...βs
dove α0 ∈{+,−},αi,βj ∈{0,1,...,b − 1} con i = 1...m e j = 1...s ed α1≠0 per la
normalizzazione.
La stringa suddetta rappresenta il numero reale:
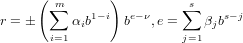 |
in cui lo shift ν è fissato e chiameremo le quantità ρ = ±∑
i=1nαib1−i mantissa e μ = e−ν
esponente del numero reale. La presenza dello shift serve a evitare di sprecare un bit
dell’esponente per discriminarne il segno.
In particolare si ha che:
−ν ≤ e ≤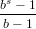 (b − 1) − ν = bs − 1 − ν
(b − 1) − ν = bs − 1 − ν
ovvero e = (b − 1)∑ j=1sbs−j − ν.
Secondo la rappresentazione appena definita, 1 ≤ ρ < b.
Dimostrazione:
Il minimo numero rappresentabile si ha nel caso α1 = 1,α2 = 0...αm = 0: 1. m−1.
m−1.
Il massimo invece si avrà nel caso α1 = ... = αm = (b − 1): (b − 1). m−1
m−1
In quest’ultimo caso si ha:
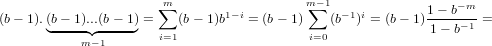 |
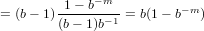 |
che è sicuramente minore di b in quanto (1 − b−m) < 1. Cvd.
Il valore assoluto minimo e massimo tra i numeri di macchina rappresentabili sono rispettivamente:
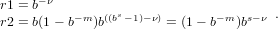 |
Definiamo adesso l’insieme dei numeri di macchina:
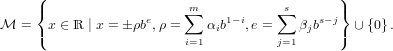 |
In particolare si ha che:
![M ⊆ [− r2,r1]∪ {0}∪ [r1,r2] = I](relazione46x.png) |
ovvero i numeri di macchina appartengono a un sottoinsieme della retta reale che per definizione è un intervallo denso, quindi infinito e non numerabile.
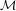 ha un numero finito di elementi.
ha un numero finito di elementi.
Infatti, α2...αmβ1...βs possono assumere bs+m−1 valori, α1 ne può assumere (b − 1) e α0
invece soltanto 2. Ovvero i numeri rappresentabili sono: 2(b − 1)bs+m−1 < 2bs+m.
In particolare |ρ| = α1α2...αm ≥ α1 ≥ 1, ma anche:
|ρ| = α1α2...αm ≤ (b − 1). m−1 ≤ b. Cvd.
m−1 ≤ b. Cvd.
In quanto 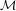 ha un numero finito di elementi e
ha un numero finito di elementi e 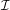 ne ha un numero infinito, è necessario
definire una funzione fl(x), detta funzione floating, che associ ad ogni numero reale x ∈
ne ha un numero infinito, è necessario
definire una funzione fl(x), detta funzione floating, che associ ad ogni numero reale x ∈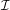 un
corrispondente numero di macchina:
un
corrispondente numero di macchina:
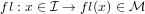 |
Sia x = ±α1α2...αmαm+1...be ∈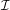
Possiamo definire:
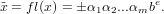 |
Sia x = ±α1α2...αmαm+1...be ∈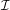
Possiamo definire
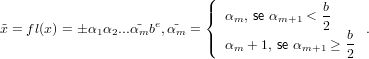 |
∀x ∈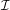 ,x≠0:
,x≠0:
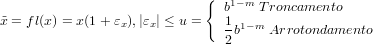 |
dove con u indichiamo la precisione di macchina.
Dimostrazione (nel caso di troncamento):
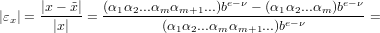 |
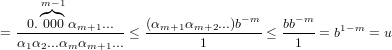 |
e quindi:
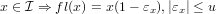 |
Osservazione: −log10|εx|≃ numero di cifre corrette nella mantissa.
In particolare −log10|εx|≤−log10|u| e m = 1 − log10|u|
La quantità u prende il nome di precisione di macchina
Dimostrazione:
nel caso di arrotondamento:
Adesso dobbiamo distinguere tra i due casi, αm+1 < 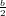 oppure αm+1 ≥
oppure αm+1 ≥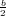 .
.
Nel primo:
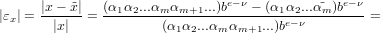 |
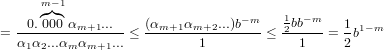 |
osservazione: (αm+1αm+2...) è minore di b∕2 per ipotesi.
Nel secondo:
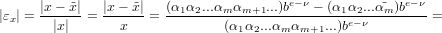 |
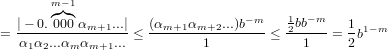 |
osservazione: (αm+1αm+2...) è sicuramente minore di b∕2.
Può capitare di dover rappresentare un numero non contenuto in 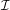 , e in questo caso ci
troveremmo in una condizione di errore. I casi possibili sono:
, e in questo caso ci
troveremmo in una condizione di errore. I casi possibili sono:
Possiamo adesso completare la definizione di fl(x):
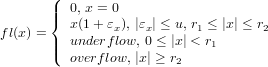 |
Lo standard IEEE 754 è stato creato per definire la rappresentazione dei numeri reali su
calcolatore, allo scopo di uniformare i risultati dei calcoli eseguiti su piattaforme
di calcolo differenti; cosa molto importante in vari ambiti scientifici è infatti la
riproducibilità del risultato. Questo standard è stato definito e ottimizzato sulla base
binaria.
Si sono scelte due rappresentazioni per i numeri reali, una a precisione singola (32 bit), e una
a doppia precisione (64 bit).
Nelle due rappresentazioni i bit sono così distribuiti:
In quanto i numeri rappresentati sono da intendersi come normalizzati, si è stabilito che α1
non venga rappresentato, in quanto sempre uguale a 1: si ottiene un bit in più
dedicabile alla mantissa, che quindi in realtà è di 24 bit per la rappresentazione
a singola precisione e di 54 per quella a doppia precisione. Indicheremo con f la
parte frazionaria della mantissa, ovvero l’unica parte rappresentata in macchina:
α2...αm.
Per poter gestire anche i casi di eccezione, è stato deciso di dedicare il primo e l’ultimo
numero rappresentabile nell’esponente a queste situazioni, ovvero:
per quanto riguarda la singola precisione e:
per quanto riguarda la doppia.
In questo modo si ottiene un range di numeri rappresentabili di circa 10−38 ÷ 1038 per i
numeri in singola precisione e 10−308 ÷ 10308 per quelli in doppia.
La rappresentazione scelta dallo standard è per arrotondamento, ma con una piccola
differenza da quello esposto precedentemente:
fl(x) è definito come il numero di macchina più vicino a x, ma in caso di due numeri di
macchina equidistanti, viene selezionato quello il cui ultimo bit della mantissa è
0:
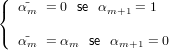
Questo tipo di arrotondamento è chiamato arrotondamento al pari (round to even).
Il più grande numero di macchina si avrà nel caso:
α0 = +; α1 = ... = αN = (b − 1); β1 = ... = βs = (b − 1);
In particolare, secondo lo standard IEEE754:
m=53, s=11, ν=1023 se il numero è normalizzato. Quindi:
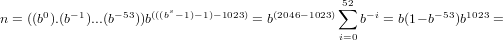 |
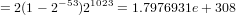 |
mentre il risultato della funzione realmax di Matlab restituisce: 1.7977e+308.
Il più piccolo numero di macchina normalizzato positivo si ha invece nel caso:
α0 = +; α1 = 1,α2 = ... = αN = 0; β1 = ... = βs−1 = 0; βs = 1.
Quindi secondo lo standard:
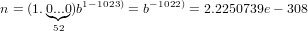 |
mentre il risultato della funzione realmin di Matlab restituisce: 2.2251e-308.
Il più piccolo numero di macchina denormalizzato si ha quando:
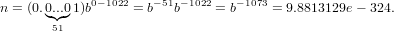 |
La precisione di macchina è:
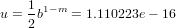 |
É importante soffermarsi sul comportamento delle operazioni elementari in aritmetica finita. Lavorando su numeri interi, se il risultato dell’operazione cade all’interno dell’insieme di rappresentabilità, le operazioni coincidono con quelle algebriche. Considerando invece i numeri interi, le operazioni saranno definite solo su numeri di macchina e dovranno avere per risultato ancora un numero di macchina; ovvero ad esempio nel caso dell’addizione si ha che x ⊕ y = fl(fl(x) + fl(y)). In particolare, le operazioni in macchina sui numeri reali generalmente non godono di tutte le usuali proprietà algebriche, come ad esempio la proprietà associativa e quella distributiva.
La conversione di tipo da intero a reale non presenta particolari problemi, in quanto, a parità di bit di rappresentazione, un intero è sempre rappresentabile in forma reale, introducendo al massimo un errore dell’ordine della precisione di macchina u: questo è infatti l’errore commesso approssimando tramite la funzione fl(x). Convertire un reale in un intero invece può causare problemi, dovuti alla grande differenza nel range di rappresentabilità: circa 1038 per i reali e circa 1010 per gli interi.
Supponiamo di dover risolvere un problema rappresentabile nella forma x = f(x), dove x
sono i dati in ingresso, y rappresenta il risultato è f è un metodo numerico. Quello che ci
troveremo in realtà a risolverein macchina è un problema del tipo ỹ = 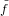 (
( ); ovvero
eseguiremo una funzione perturbata (con operazioni eseguite in aritmetica finita, con possibile
errori di discretizzazione e/o convergenza) su un dato perturbato (errore di rappresentazione
sempre presente, possibile origine sperimentale del dato). Per semplicità ci limiteremo a
studiare il problema ỹ = f(
); ovvero
eseguiremo una funzione perturbata (con operazioni eseguite in aritmetica finita, con possibile
errori di discretizzazione e/o convergenza) su un dato perturbato (errore di rappresentazione
sempre presente, possibile origine sperimentale del dato). Per semplicità ci limiteremo a
studiare il problema ỹ = f( ), ovvero considereremo il metodo numerico come eseguito in
aritmetica esatta.
), ovvero considereremo il metodo numerico come eseguito in
aritmetica esatta.
Consideriamo quindi le grandezze  = x(1 + εx) e ỹ = y(1 + εy) e studiamo la relazione che
intercorre tra l’errore relativo in ingresso e quello in uscita, considerando un’analisi al primo
ordine:
= x(1 + εx) e ỹ = y(1 + εy) e studiamo la relazione che
intercorre tra l’errore relativo in ingresso e quello in uscita, considerando un’analisi al primo
ordine:
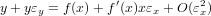 |
ovvero:
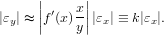 |
Il valore di amplificazione k, che indica quanto gli errori iniziali possano essere amplificati sul risultato finale, è denominato numero di condizionamento del problema.
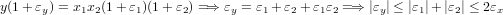 |
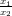
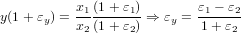 |
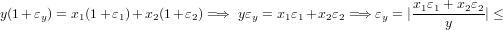 |
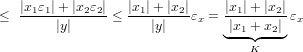 |
Mentre la moltiplicazione è ben condizionata vediamo che nel caso della somma dobbiamo differenziare due casi:
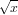
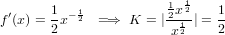 |
Il codice Matlab:
esegue un loop infinito. Questo perché il numero 0.1 non è rappresentabile in base binaria come numero finito ma solo come numero periodico, e quindi subisce un errore di approssimazione. In questo modo sommando ripetutamente 0.1 in binario non si arriva mai esattamente ad 1 e quindi il ciclo non si ferma. Questo codice potrebbe essere corretto sostituendo il controllo x≠1 con x <= 1, ma questo non garantisce che venga eseguito esattamente lo stesso numero di cicli che sarebbe stato eseguito dal codice precedente se avesse funzionato.
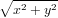 :
:Calcolare 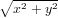 eseguendo
eseguendo 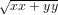 non è il migliore dei modi: infatti, in caso
x = y = r1,fl(x) = fl(y) = 0,fl(
non è il migliore dei modi: infatti, in caso
x = y = r1,fl(x) = fl(y) = 0,fl(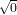 ) = 0, oppure se x è vicino ad r2, x2 non può essere
rappresentato. Questo problema può essere risolto in modo più efficiente eseguendolo invece
in questo modo:
) = 0, oppure se x è vicino ad r2, x2 non può essere
rappresentato. Questo problema può essere risolto in modo più efficiente eseguendolo invece
in questo modo:
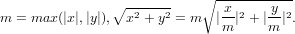 |
che permette di effettuare il calcolo anche nelle condizioni estreme sopra descritte.
Eseguendo in matlab il codice:
La variabile eps rappresenta la precisione di macchina. Più precisamente è il più largo spazio relativo tra due numeri adiacenti del sistema floating point della macchina. Questo numero è ovviamente dipendente dalla macchina, ma in macchine che supportano l’aritmetica floating point IEEE 64 bit, vale approssimativamente 2.2204e-16. Le due istruzioni sopra descritte danno come risultato:
Ovvero non vale la proprietà associativa. Nel caso invece:
si hanno i seguenti risultati:
Ovvero nel primo caso l’operazione viene eseguita correttamente, mentre nel secondo si incorre in overflow e non è possibile svolgere il calcolo e quindi non vale la proprietà distributiva.
Supponiamo di voler calcolare: y = 0.12345678 − 0.12341234 ≡ 0.00004444, utilizzando una
rappresentazione decimale con arrotondamento alla quarta cifra significativa.
Otteniamo ỹ = 1.235 ∗ 10−1 − 1.234 ∗ 10−1 = 1 ∗ 10−4.
L’errore relativo su y é:
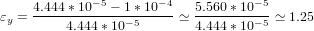 |
mentre essendo εx1 = 3.5 ∗ 10−4 e εx2 = −1 ∗ 10−4, si ha che
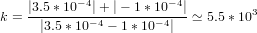 |
Il problema risulta essere mal condizionato.
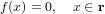 |
in cui f : ℝ→ℝè una funzione assegnata; ovvero siamo interressati a trovare, se esiste, uno zero reale della funzione. In generale ci possiamo trovare in tre diverse situazioni:
In particolare ci limiteremo a lavorare su funzioni tali che, definito [a,b] intervallo in ℝ con a < b, queste godano di certe proprietà:
Questo garantisce l’esistenza di una radice di f all’interno dell’intervallo [a,b], ovvero la funzione,
passando da positiva a negativa all’interno di questo intervallo, deve necessariamente
attraversare l’asse delle ascisse in almeno un punto.
Come primo passo dobbiamo scegliere un punto interno all’intervallo che sia una
miglior approssimazione della radice (), in particolare scegliamo il punto medio:
x1 = 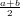 .
.
A questo punto possono verificarsi solo tre casi:
Con questo metodo si ha che | − x1|≤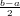 . Ragionando per induzione, indicando con
[ai,bi] l’intervallo di confidenza e con xi = (ai + bi)∕2 l’approssimazione della radice
all’intervallo i-esimo, si ha che:
. Ragionando per induzione, indicando con
[ai,bi] l’intervallo di confidenza e con xi = (ai + bi)∕2 l’approssimazione della radice
all’intervallo i-esimo, si ha che:
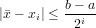 |
Ovvero ad ogni iterazione si dimezza la distanza massima della serie dalla soluzione. In questo modo, si può pensare di voler ottenere il calcolo di una approssimazione della radice che disti al più tolx dalla radice,e si ha che questa si raggiunge in un numero di iterazioni:
![imax ≡ [log2(b− a)− log2(tolx)]](relazione92x.png) |
Adesso sappiamo che sicuramente, dopo imax itarazioni, abbiamo raggiunto la precisione richiesta; ma possiamo ancora stabilire un criterio efficace per accorgersi se si è arrivati sufficientemene vicini alla soluzione prima di imax iterazioni. In linea di massima, se f() = 0, per la continuità di f si deve avere che il valore che la funzione assume in prossimità di x debba assumere valori vicini a 0. In questo modo possiamo pensare ad un controllo di arresto del tipo |f(x)| < tolf dove tolf deve essere scelta in modo da avere |x −| < tolx. Supponendo f ∈ C(1), sviluppando in serie di Taylor:
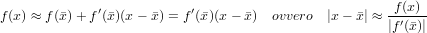 |
e quindi tolf ≈|f′()|tolx.
Tanto più grande sarà |f′()|, tanto meno stringente dovrà essere il criterio di arresto sulla funzione. Infatti si ha che:
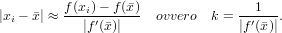 |
dove k rappresenta il numero di condizionamento del problema. Questo metodo sarà ben condizionato in presenza di funzioni che hanno una derivata prima molto grande nei pressi della radice, ma mal condizionato quando questa si avvicina o tende a zero.
Considerando che una buona approssimazione di f′() è ricavabile, a costo molto basso, in questo modo:
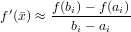 |
si può pensare al seguente algoritmo per l’applicazione del metodo di bisezione:
Per quanto riguarda il costo di questo algoritmo in termini di operazioni floating-point, si vede facilmente dal codice che questo algoritmo ad ogni ciclo esegue esattamente 3 somme, 4 moltiplicazioni ed una valutazione di funzione, tutto questo al massimo imax volte. Tenendo conto che imax è definito come log2(b − a) − log2(tolx), si può affermare che questo algoritmo ha un costo di andamento grossomodo logaritmico all’allargarsi dell’intervallo di confidenza. Il costo in termini di memoria è anch’esso molto contenuto, si utilizzano infatto soltanto poche variabili.
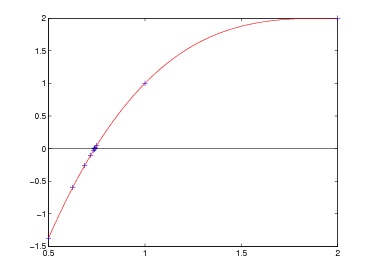
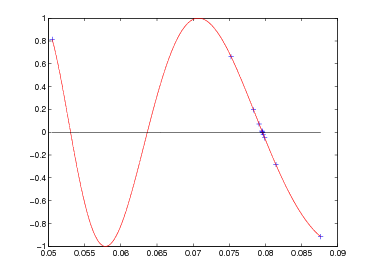
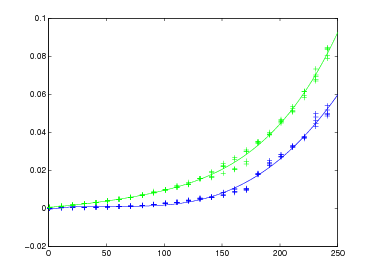
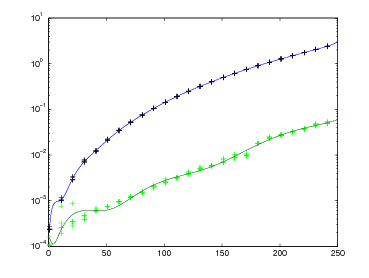
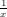 ) con
l’intervallo di partenza [10−3,10−1].
) con
l’intervallo di partenza [10−3,10−1].
Definito come ei = xi − l’errore commesso al passo i-esimo nell’approssimazione fornita da un dato metodo numerico, questo medoto è convergente se:
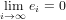 |
Il metodo ha ordine di convergenza p ∈ℝ se p è il più grande numero positivo per cui:
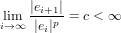 |
dove c e detta costante asintotica dell’errore. In particolare si avranno metodi che convergono linearmente quando p = 1, esponenzialmente (quadraticamente, cubicamente...) per p > 1, e metodi non convergenti se p < 1.
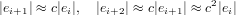 |
ovvero, per induzione:
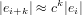 |
Abbiamo quindi che per i molto grandi, ovvero dopo molte iterazioni, anche k è molto grande, e si deve avere che 0 ≤ c ≤ 1 altrimenti la funzione sarebbe divergente.
Il metodo di Newton si basa sull’idea di sfruttare, come successiva approssimazione della radice, il punto di intersezione della retta tangente alla funzione nel punto (x0,f(x0)) con l’asse delle ascisse, considerando x0 l’approssimazione iniziale. Consideriamo quindi y = f(xi) + f′(xi)(x − xi), ponendo y a zero si ha che:
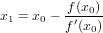 |
che è definita per f′(x0)≠0. Possiamo estendere il ragionamento a tutti i passi successivi:
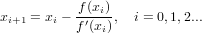 |
Se xi è la successione sopre descritta, che converge a , zero semplice di f(x)
funzione di classe 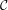 2, allora il metodo di Newton converge almeno quadraticamente.
2, allora il metodo di Newton converge almeno quadraticamente.
Dim.
Per ipotesi abbiamo che xi → per i →∞. Quindi:
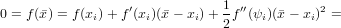 |
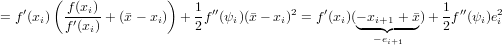 |
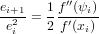 |
che è ben definita in quanto f′(xi) è sicuramente diverso da zero perché stiamo trattando il caso di una radice semplice e siamo in un opportuno intorno di , e se il metodo converge si ha:
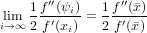 |
Se xi → con i →∞ radice di molteplicità m > 1, allora l’ordine di convergenza del metodo di Newton è solo lineare (p = 1) con c = (m − 1)∕m
Rimane ancora da stabilire quali siano le condizione sufficienti a garantire la convergenza del metodo verso la soluzione. Per prima cosa è necessario formalizzare un metodo iterativo per approssimare una radice dell’equazione f(x) = 0:
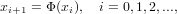 |
ed ovviamente la radice deve essere un punto fisso per questa funzione di iterazione. Possiamo quindi definire la funzione di iterazione per il metodo di Newton:
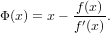 |
Sia Φ(x) la funzione di iterazione che definisce un metodo numerico. Supponiamo che
∃ δ > 0,0 ≤ L < 1 tali che ∀x,y ∈ ( − δ, + δ) ≡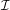 ; |Φ(x) − Φ(y)|≤ L|x − y|
; |Φ(x) − Φ(y)|≤ L|x − y|
allora:
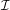
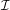 ⇒ xi ∈
⇒ xi ∈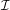 ∀i ≥ 0
∀i ≥ 0
Dim(1).
Supponiamo per assurdo che ∃  |
|  ≡ Φ(
≡ Φ( ) ∈
) ∈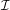 ulteriore punto fisso per Φ, ovviamente
≠
ulteriore punto fisso per Φ, ovviamente
≠ . Ma allora si ha che: 0 < | −
. Ma allora si ha che: 0 < | − | = |Φ() − Φ(
| = |Φ() − Φ( )|≤ L| −
)|≤ L| − | ma essendo L < 1 si ha
che | −
| ma essendo L < 1 si ha
che | − | < | −
| < | − |, assurdo.
|, assurdo.
Dim(2).
Sia x0 ∈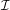 ⇐⇒| − x0| < δ.
⇐⇒| − x0| < δ.
Allora: | − xi| < δ e | − xi| = |Φ() − Φ(x0)|≤ L| − x0| < Lδ < δ
e xi ∈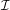 .
.
Dim(3).
|xi −| = |Φ(xi−1) − Φ()|≤ L|xi−1 −|, ovvero:
|xi −| = L|Φ(xi−2) − Φ()|≤ L2|xi−2 −|
Ragionando per induzione possiamo quindi concludere che:
|xi −|≤ Li|x0 −|, che tende a zero per i che tende a infinito.
Se si assume f(x) ∈ C(2), tramite questo teorema è possibile dimostrare la convergenza
locale del metodo di Newton. In questo caso infatti la funzione di iterazione è di classe C(1)
e Φ′() = 0. Fissato quindi un arbitrario L ∈ [0,1), esisterà un δ > 0 tale che
|Φ′(x)|≤ L,∀x ∈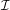 ≡ (−δ, + δ). Sviluppando in serie di Taylor al primo ordine si ottiene
che:
≡ (−δ, + δ). Sviluppando in serie di Taylor al primo ordine si ottiene
che:
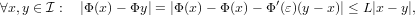 |
con ε compreso tra x e y ovvero apppartenente ad 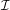 . La funzione di iterazione soddisfa le
ipotesi del teorema, e quindi il metodo di Newton è localmente convergente se
x0 ∈
. La funzione di iterazione soddisfa le
ipotesi del teorema, e quindi il metodo di Newton è localmente convergente se
x0 ∈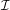
Differentemente dal metodo di bisezione, a causa della convergenza solo locale del metodo di Newton, non è possibile stabilire a priori il numero massimo di iterazioni necessarie per raggiungere la soluzione con l’accuratezza richiesta. Come nel caso precedente vorremmo stabilire un criterio sulla dimensione dell’errore, ovvero vogliamo fermarci quando |ei|≤ tolx dove tolx rappresenta appunto la tolleranza che siamo disposti ad accettare intorno alla soluzione. Notiamo che nel caso di convergenza verso radici semplici il metodo di Newton converge quadraticamente ed in prossimità della radice si ha:
 |
e quindi un controllo del tipo |xi+1 − xi| < tolx è appropriato ed equivalente al
controllo |f(xi)|≤|f′(xi)|tolx in quanto xi+1 = xi −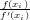 . Bisogna notare però che
questo controllo essenzialmente non è altro che una verifica sull’errore assoluto
su x, ovvero tolx ≃ O(x). Benché questo possa risultare appropriato per valori
piccoli di x, non lo è necessariamente anche per valori grandi, dove risulta molto più
efficiente un controllo sull’errore relativo. Possiamo quindi definire la grandezza
“errore relativo su x” come |ei|≤ rtol||≈ rtol|xi+1|, ed un criterio di arresto del
tipo:
. Bisogna notare però che
questo controllo essenzialmente non è altro che una verifica sull’errore assoluto
su x, ovvero tolx ≃ O(x). Benché questo possa risultare appropriato per valori
piccoli di x, non lo è necessariamente anche per valori grandi, dove risulta molto più
efficiente un controllo sull’errore relativo. Possiamo quindi definire la grandezza
“errore relativo su x” come |ei|≤ rtol||≈ rtol|xi+1|, ed un criterio di arresto del
tipo:
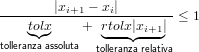 |
che è un criterio di arrsto ibrido che si arresta quando è soddisfatto il criterio più stringente. In particolare si ha che per valori piccoli di x, rtolx|xi+1|è un valore piccolo rispetto ad x e quindi il criterio assoluto predomina, viceversa invece per valori di x grandi; ponendo rtolx uguale a zero questo criterio ritorna equilvalente a |xi+1 − xi| < tolx.
Quando la convergenza del metodo è solo lineare, il criterio di arresto può essere modificato. Si ha infatti che:
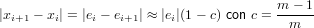 |
Noi vogliamo |ei| < tolx e quindi:
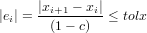 |
Ovvero abbiamo ottenuto un criterio tanto più efficiente quanto più la molteplicità della
radice è alta (c ≈ 1). Noi conosciamo xi+1, e vogliamo che |ei+1|≤ tolx ma sappiamo che
|ei+1| = c|ei| e possiamo quindi controllare 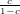 |xi+1 − xi|≤ tolx. Il problema è che non
conosciamo c. Possiamo però calcolare le prime tre iterazioni (x0,x1,x2) in questo modo:
|x1 −x0|≈ (1 −c)|e0|; |x2 −x1|≈ (1 −c)|e1|≈ (1 −c)c|e0|; e quindi c ≈
|xi+1 − xi|≤ tolx. Il problema è che non
conosciamo c. Possiamo però calcolare le prime tre iterazioni (x0,x1,x2) in questo modo:
|x1 −x0|≈ (1 −c)|e0|; |x2 −x1|≈ (1 −c)|e1|≈ (1 −c)c|e0|; e quindi c ≈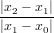 .
.
Visto quanto detto fino ad ora, possiamo pensare alla seguente implementazione del metodo
di Newton:
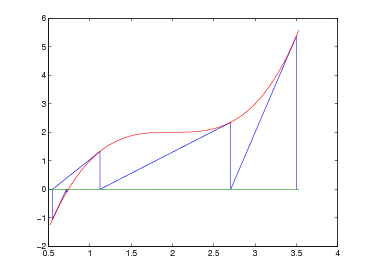
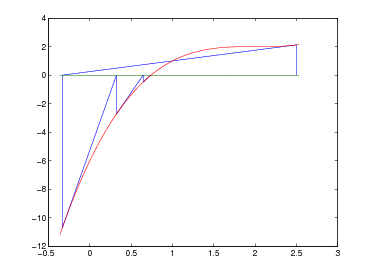
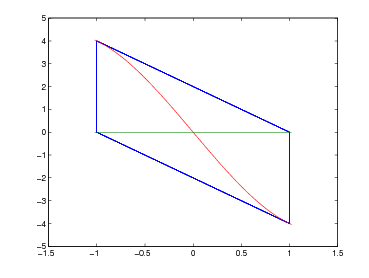
Rispetto al metodo di bisezione il metodo di Newton ha un costo leggermente più alto: questo richiede infatti 7 operazioni floating-point e due valutazioni di funzione ad ogni iterazione. In questo caso il costo massimo della determinazione dello zero non è determinabile a priori, e dipende dalla scelta di itmax effettuata dall’utente. Il costo in termini di memoria, come nel caso del metodo di bisezione è anch’esso molto contenuto e si utilizzano soltanto poche variabili.
Una radice ha moltiplicità esatta m se:
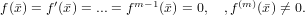 |
Se f(x) è sviluppabile in serie di Taylor in , sua radice di molteplicità esatta m, allora è scrivibile nella forma f(x) = (x−)mg(x) con g(x) ancora sviluppabile in serie di Taylor in e tale che g()≠0.
Supponiamo di avere una radice di molteplicità nota m. Allora f(x) sarà del tipo (x−)m. Avendo x0 approssimazione di :
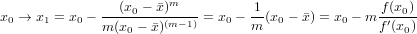 |
ovvero
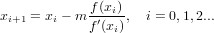 |
In questo caso particolare si riesce ad ottenere la convergenza alla radice in un solo passo
iterativo, utilizzando il fattore di correzione m.
In generale, f(x) è una funzione del tipo (x −)mg(x) (con g(x) qualsiasi) e non
si riesce quindi ad ottenere il risultato in un solo passo iterativo come nel caso
particolare detto sopra; è dimostrabile che questa modifica riesce però a ripristinare la
convergenza quadratica del metodo di Newton verso radici di molteplicità nota.
Supponiamo invece di avere una radice di molteplicità ignota. In questo caso al generico passo i-esimo si ha che ei ≈ cei−1 ed ei+1 ≈ cei, con c costante asintotica dell’errore, incognita. Dalla combinazione delle due si ottiene che ei+1ei−1 ≈ ei2 e quindi (xi+1 −)(xi−1 −) ≈ (xi −)2. Se si suppone esatta l’uguaglianza, si ha che:
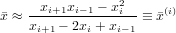 |
In questo modo si può pensare ad una macchinetta iterativa che agisce su due livelli:
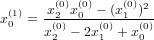 |
si ottiene una successiva approssimazione più accurata x0(1) della radice da utilizzare per il successivo ciclo interno. Questo sistema, chiamato “metodo di accelerazione di Aitken”, permette di ripristinare la convergenza quadratica del metodo di newton nel caso di radici multiple di molteplicità ignota, al prezzo di aumentare il numero di operazioni da eseguire ad ogni iterazione (ciclo a due livelli).
Come descritto nella teoria, questo algoritmo effettua, ad ogni iterazione, due passi del metodo di Newton ed un passo di accelerazione, per un costo totale quindi di 16 operazioni floating point e 4 valutazioni di funzione. Per quanto riguarda l’occupazione di memoria, anche qui usiamo solo poche variabili.
I metodi detti quasi-Newtoniani sono delle varianti del metodo di Newton che permettono di risparmiare il calcodo della derivata prima della funzione ad ogni passo iterativo. Questi metodi sono descrivibili tramite uno schema generale che li accomuna:
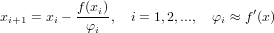 |
Questo metodo si basa sull’osservazione che, in prossimità della radice, la derivata prima della funzione in esame varia di poco, e si può quindi pensare di calcolarla una sola volta e di utilizzare poi un fascio di rette parallele a questa per approssimarla nelle iterazioni successive. Supponendo di essere in presenza su una funzione sufficientemente regolare ed abbastanza vicini alla radice, si può definire il metodo come:
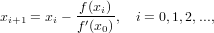 |
Il vantaggio di questo metodo risiede nel basso costo computazionale per iterazione (si valuta solo una volta f′(x) e una sola volta per iterazione f(x)), ma si può dimostrare che l’ordine di convergenza è solo lineare.
Questo metodo ad ogni ciclo iterativo svolge soltanto 7 operazioni floating point ed una valutazione di funzione, il costo per iterata è quindi molto basso. Bisogna inoltre notare come la convergenza del metodo sia molto legata al tipo di funzione e alla scelta del punto di partenza; se questo non è abbastanza vicino alla radice oppure la funzione non è abbastanza regolare, il mtodo può convergere molto lentamente.
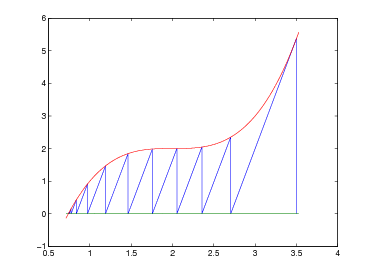
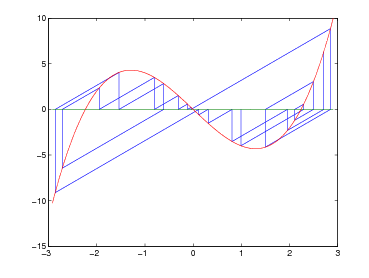
Tenendo conto della definizione della derivata prima mediante rapporto incrementale, si può pensare di sfruttare due approssimazioni successive (ovvero due precedenti valutazioni di f(x)) per approssimarla. Considerando quindi di essere all’iterazione i-esima e di aver già calcolato xi−1,xi,f(xi−1),f(xi), si approssima f′(x) in questo modo:
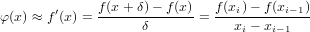 |
Il metodo iterativo risultante:
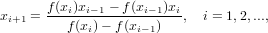 |
con x0,x1 approssimazioni iniziali assegnate.
In questo modo si ha la possibilità di calcolare una sola volta per itearazione il valore
di f(x), ottenendo così un metodo con costo per iterazione molto basso; in più,
quando la funzione stà convergendo si ha che xn è molto vicino a xn−1, e il rapporto
incrementale risulta una buona approssimazione per la derivata. Questo metodo è
caratterizzato da un’ordine di convergenza 1 ≤ p ≤ 2; in particolare si può dimostrare che
p = 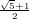 ≈ 1,618 nel caso di radici semplici, ma è solo lineare nel caso di radici
multiple.
≈ 1,618 nel caso di radici semplici, ma è solo lineare nel caso di radici
multiple.
Questo metodo ad ogni ciclo iterativo svolge soltanto 5 operazioni floating point ed una valutazione di funzione, il costo per iterata è quindi veramente molto basso.
Queste tabelle mostrano il comportamento di questi tre metodi nella valutazione delle funzioni:
 |
per valori decrescenti della tolleranza tolx e punto iniziale x0 = 10.
| f1(x) | f2(x) | |||||
| tolx | i | x | tolx | i | x | |
| NTN | ||||||
| 10−2 | 43 | 1.08727963568088 | 10−2 | 52 | 1.08957265092411 | |
| 10−4 | 87 | 1.00084641497829 | 10−4 | 96 | 1.00087725269306 | |
| 10−6 | 131 | 1.00000820831010 | 10−6 | 140 | 1.00000850818739 | |
| 10−8 | 174 | 1.00000008844671 | 10−8 | 184 | 1.00000008251024 | |
| 10−10 | 218 | 1.00000000085773 | 10−10 | 227 | 1.00000000088907 | |
| NTM | ||||||
| 10−2 | 1 | 1 | 10−2 | 4 | 1.00000041794715 | |
| 10−4 | 1 | 1 | 10−4 | 5 | 1.00000000000002 | |
| 10−6 | 1 | 1 | 10−6 | 5 | 1.00000000000002 | |
| 10−8 | 1 | 1 | 10−8 | 6 | 1 | |
| 10−10 | 1 | 1 | 10−10 | 6 | 1 | |
| ATK | ||||||
| 10−2 | 2 | 1 | 10−2 | 6 | 0.99999998332890 | |
| 10−4 | 2 | 1 | 10−4 | 7 | 1 | |
| 10−6 | 2 | 1 | 10−6 | 7 | 1 | |
| 10−8 | 2 | 1 | 10−8 | 7 | 1 | |
| 10−10 | 2 | 1 | 10−10 | 7 | 1 | |
Questa tabella mostra il comportamento di questi metodi nella valutazione della funzione:
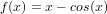 |
per valori decrescenti della tolleranza tolx e punto iniziale x0 = 0, mentre per il metodo di bisezione consideriamo l’intervallo [0,1].
| f(x) | ||
| tolx | i | x |
| NTN | ||
| 10−2 | 3 | 0.73908513338528 |
| 10−4 | 3 | 0.73908513338528 |
| 10−6 | 4 | 0.73908513321516 |
| 10−8 | 4 | 0.73908513321516 |
| 10−10 | 5 | 0.73908513321516 |
| SCT | ||
| 10−2 | 3. | 0.73911936191163 |
| 10−4 | 4 | 0.73908511212746 |
| 10−6 | 5 | 0.73908513321500 |
| 10−8 | 6 | 0.73908513321516 |
| 10−10 | 6 | 0.73908513321516 |
| CRD | ||
| 10−2 | 12 | 0.73560474043635 |
| 10−4 | 24 | 0.73905479074692 |
| 10−6 | 35 | 0.73908552636192 |
| 10−8 | 47 | 0.73908513664657 |
| 10−10 | 59 | 0.73908513324511 |
| BIS | ||
| 10−2 | 7 | 0.734375 |
| 10−4 | 13 | 0.739013671875 |
| 10−6 | 20 | 0.73908424377441 |
| 10−8 | 25 | 0.73908513784409 |
| 10−10 | 31 | 0.73908513318747 |
 |
dove A = (aij) ∈ℝm×n matrice dei coefficienti, b = (bi) ∈ℝm vettore dei termini noti e x = (xi) ∈ℝn vettore delle incognite. Assumeremo che la matrice abbia un numero di righe maggiore o uguale a quello delle colonne (m ≥ n) e che abbia rango massimo (rank(A) = n); queste assunzioni riescono comunque a coprire una buona parte dei problemi derivati dalle applicazioni.
Iniziamo esaminando il caso in cui m = n, ovvero A è una matrice quadrata. In quanto rank(A) = n, A è una matrice nonsisngolare e la soluzione del sistame esiste ed è unica:
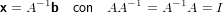 |
Analizziamo adesso il caso in cui A sia una matrice diagonale, ovvero:
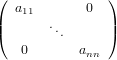 |
in cui valgono le proprietà:
 aii≠0 ∀i,0 ≤ i ≤ n.
aii≠0 ∀i,0 ≤ i ≤ n.
In questo caso il sistema lineare Ax = b assume la forma:
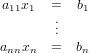 |
e quindi la soluzione ottenibile:
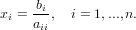 |
è ben posta in quanto come detto prima aii≠0 per i = 1,...,n. Il costo di questo metodo sia in termini di occupazione di memeoria che di quantità di operazioni floating-point è lineare con la dimensione del problema; sono sufficiendi n operazioni floating-point ed un vettore di dimensione n per memorizzare gli elementi della diagonale della matrice A.
Le matrici triangolari, che contengono informazione soltanto in una porzione triangolare, possono essere di due tipi:
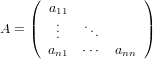 |
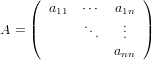 |
Nel caso in cui la matrice A sia triangolare inferiore (il caso in cui sia triangolare superiore è analogo) il sistema lineare è della forma:
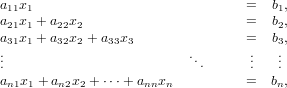 |
e quindi le soluzioni sono ottenibili tramie sostituzioni successive in avanti:
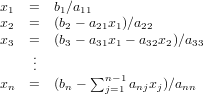 |
In quanto A è nonsingolare, si ha che aii≠0, i = 1,...,n e quindi tutte le operazioni sopra descritte sono ben definite. In quanto la matrice contiene informazione solo in una sua porzione triangolare, è sufficiente memorizzare tale porzione che contiene:
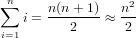 |
posizioni di memoria. Per quanto riguarda il costo computazionale invece, da quanto detto sopra si ha che sono necessari 1flop per calcolare x1,3flop per calcolare x2,...,2n− 1flop per calcolare xn, e quindi:
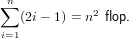 |
Una matrice è ortogonale se e solo se vale la proprietà: A−1 = AT. In questo caso quindi la soluzione del sistema lineare è ottenibile facilmente calcolando x = ATb, al costo di un prodotto matrice-vettore; saranno richiesti pertanto circa 2n2flops ed n2 posizioni di memoria.
Mostriamo adesso alcune proprietà interessanti di questi tipi di matrici che andremo ad
utilizzare con i metodi di fattorizzazione.
La somma ed il prodotto di matrici triangolari inferiori (superiori) è ancora una matrice
triangolare inferiore (superiore).
Dimostrazione:
Dimostriamo il caso con matrici triangolari inferiori, l’altro si domostra in maniera analoga.
Siano L1,L2 matrici triangolari inferiori, ed indichiamo con (aij) e (bij i corrispettivi
elementi.
Per ipotesi abbiamo che aij = bij = 0, j > i.
Allora gli elementi della matrice somma saranno composti:
L1 + L2 = (aij + bij) ma se j > i si ha (aij + bij) = 0 + 0 = 0, ovvero L1 + L2 è triangolare
inferiore.
Vediamo adesso il caso del prodotto.
Chiamaiamo cij gli elementi della matrice L1L2. Vogliamo dimostrare che cij = 0, se
j > i.
L’elemento cij, quando j > i, è scrivibile nella forma: eiT(L1L2)ej. Svolgendo le operazioni
in quest’ordine: (eiTL1)(L2ej) si ha:
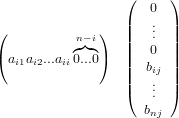 |
ed il vettore b contiene 0 nelle prime j − 1 posizioni. Ma j > i e quindi i primi j
zero del vettore b annullano tutti i termini diversi da zero del vettore a, e cij = 0.
Se L1 = (aij)eL2 = (bij) sono matrici triangolari inferiori, allora gli elementi diagonali della
matrice L1L2 sono dati da (aiibii).
Dimostrazione:
Sia cij elemento della matrice risultante. Per definizione di prodotto tra matrici, si ha
che
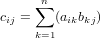 |
Ricordando che aij = bij = 0 se j > i, si nota facilmente che la somma non è interessata elementi che coinvolgono valori di k minori di j o maggiori di i in quanto il prodotto è annullato dall’elemento rispettivamente della matrice L2 o L1; l’unico prodotto che non si annulla quando i = j (stiamo calcolando la diagonale) si ha con k = i = j e coinvolge appunto solamente i fattori akk e bkk. Cvd.
La somma ed il prodotto di matrici triangolari inferiori (o superiori) è ancora una matrice
dello stesso tipo.
Dimostrazione:
Siano L ed S due matrici tiangolari inferiori. Se i < j quindi L(i,j) = S(i,j) = 0, e
sommandole, si ha quindi che L + S(i,j) = L(i,j) + S(i,j) = 0 + 0 = 0, ovvero
anche la loro somma è una matrice triangolare inferiore. Nel caso del prodotto si ha
che
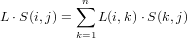 |
ma se i < j, L(i,j) = S(i,j) = 0 e quindi S(k,j) = 0 per k < j e L(i,k) = 0 per ,k > i e tutti i prodotti si annullano. Lo stesso ragionamento vale per matrici triangolari superiori, con i > j.
Il prodotto di due matrici triangolari inferiori (o superiori) a diagonale unitaria è ancora una
matrice dello stesso tipo.
Dimostrazione:
Abbiamo appena dimostrato che il prodotto conserva la triangolarità, vediamo cosa succede
alla diagonale:
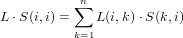 |
ma in questo caso l’unico elemento non nullo nella sommatoria è L(1,1) ⋅ S(1,1,) = 1.
Se L è nonsingolare e triangolare allora L−1 è triangolare dello stesso tipo.
Dimostrazione:
Supponiamo L triangolare inferiore e L−1 triangolare superiore. Allora si avrebbe che
(L⋅L−1)(1,2) = L(1,1) ∗L−1(1,1) + 0 + 0≠0, in quanto per ipotesi L(1,1),L−1(1,1)≠0. Ne
consegue risultato non può essere la matrice identità, e l’inversa di una matrice triangolare
deve pertanto essere anch’essa triangolare dello stesso tipo.
Questo codice implementa gli algoritmi di risoluzione dei sistemi lineari di tipo semplice, quali i triangolari inferiori e superiori, diagonale, ortogonale e bidiagonale superiore e inferiore.
Da quanto descritto fino ad ora si può concludere che siamo in grado di trattare in maniera efficiente matrici particolari quali quelle diagonali e quelle triangolari. Ovviamente non tutte le matrici sono di questi tipi, ma siamo in grado di definire alcuni metodi, detti di fattorizzazione, che permettodo di descrivere una matrice generica come prodotto di fattori che siano matrici particolari, ovvero del tipo a noi più congeniale. Vogliamo quindi poter scrivere A = F1F2...Fk,dove Fk ∈ℝn×n sono matrici diagonali, triangolari oppure ortogonali. In questo modo, tenendo conto della fattorizzazione di A, è possibile risolvere il sistema Ax = b nel seguente modo:
 |
É importante notare che tutti i sistemi appena citati sono di tipo semplice e quindi immediatamente risolvibili, e che non è necessario memorizzare tutte le soluzioni intermedie, perché queste perdono di utilità una volta calcolata quella successiva.
In base a quanto detto fin’ora, una situazione interessante si ha quando stiamo lavorando su di una matrice A che può essere scritta come il prodotto di due matrici particolari che noi chiameremo Lower ed Upper, tali che L sia triangolare inferiore a diagonale unitaria e U triangolare superiore; ovvero la matrice A è fattorizzabile LU.
Se A è una matrice nonsingolare e la fattorizzazione A = LU esiste , allora questa è
unica.
Dimostrazione:
Siano A = L1U1 = L2U2 due fattorizzazioni di A; si ha che:
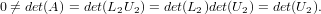 |
U2 è quindi nonsingolare e si ha che L1−1L2 = U1U2−1 ≡ D. Ma L1−1L2 e U1U2−1
sono rispettivamente triangolare inferiore e triangolare superiore, pertanto D deve
essere diagonale. Ma L1−1L2 è una matrice a diagonale unitaria e questo implica
che D sia la matrice Identità; ne consegue quindi che L1 = L2 e U1 = U2. cvd.
Rimane adesso da stabilire l’esistenza di tale fattorizzazione, e procederemo illustrando un
metodo di fattorizzazione.
Sia v = (v1...vn)T ∈ℝn vettore tale che vk≠0, si supponga di volerne azzerare tutte le
componenti successive alla k-esima esclusa, lasciando invariate tutte le altre, moltiplicandolo
a sinistra con una matrice triangolare inferiore a diagonale unitaria L ∈ℝn×n. É possibile
definire il vettore elementare di Gauss come:
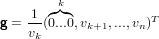 |
grazie al fatto di avere vk≠0, e quindi la matrice elementare di Gauss:
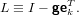 |
Ovvero:
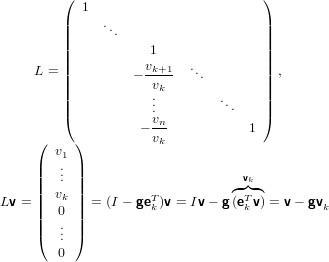 |
Questa matrice opera come ci eravamo preposti, infatti le prime k componenti del vettore
Lv coincidono con le rispettive di v.
L’inversa di L è facilmente ottenibile come: L−1 = I + gekT, infatti:
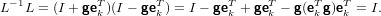 |
in quando ekTg,k-esima componente del vettore g, è nulla.
Procediamo adesso alla trasformazione della matrice nonsingolare A in una matrice
triangolare superiore mediante la procedura iterativa denominata metodo di eliminazione di
Gauss, che dura n − 1 passi.
Definiamo:
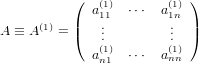 |
la matrice al primo passo. L’indice superiore di ciascun elemento tiene traccia del passo più
recente in cui il valore dell’elemento è stato modificato dalla procedura. Vogliamo quindi
come primo passo definire una matrice triangolare inferiore a diagonale unitaria che sia in
grado di trasformare A rendendo la prima colonna strutturalmente uguale alla relativa di una
matrice triangolare superiore.
Se a11(1)≠0, possiamo definire il primo vettore elementare di Gauss:
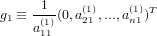 |
e la prima matrice elementare di Gauss:
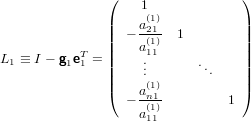 |
per avere:
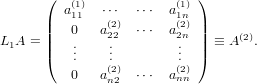 |
Possiamo osservare come, per la struttura di L, la prima riga del prodotto L1A non venga
modificata.
Generalizziamo quindi lo stesso procedimento al passo i-esimo, tenendo conto che ajj(j)≠0
per ogni j < i:
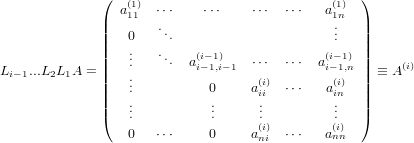 |
A questo punto solo se aii(i)≠0 sarà possibile definire l’i-esimo vettore di Gauss:
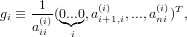 |
e quindi la i-esima matrice elementare di Gauss:
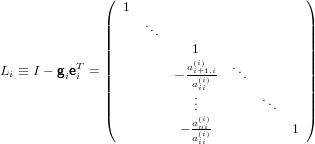 |
e quindi:
 |
Se si osserva che nella i-esima matrice di Gauss (Li ≡ I −gieiT)) le prime i righe
corrispondono con quelle della matrice identità, si può notare che le prime i righe
delle matrici A(i) e A(i+1) coincidono e gli elementi azzerati al passo i-esimo (che
stanno nelle prime i − 1 colonne) non vengono alterati dalla moltiplicazione per
Li.
Se risulta possibile iterare i passi fin qui descritti i = n − 1 volte, si ottiene che:
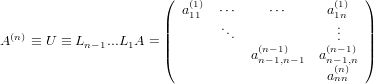 |
Adesso, osservando che la matrice Ln−1...L1 è il prodotto di matrici triangolari inferiori a diagonale unitaria, è anch’essa di questo tipo, e così sarà anche la sua inversa. Tenendo conto che:
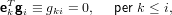 |
e ponendo formalmente la matrice Ln−1...L1 uguale a L−1:
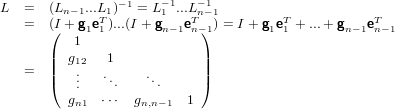 |
Siamo quindi riusciti ad ottenere due matrici L ed U tali che A = LU.
Consideriamo adesso le condizioni sufficienti a garantire l’esistenza della fattorizzazione LU: il
metodo di eliminazione di Gauss è definito se e solo se è possibile costruire la matrice di
Gauss al generico passo i-esimo.
Se A è una matrice nonsingolare, la fattorizzazione A = LU è definita se e soltanto se
aii(i)≠0, i = 1,2,...,n, ovvero se e solo se la matrice U è nonsingolare.
Si dice sottomatrice principale di ordine k di una generica matrice A ∈ℝn×n l’intersezione tra le sue prime k righe e k colonne, ovvero:
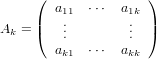 |
In particolare si ha che il determinante det(Ak) è il minore principale di ordine k di A.
Una matrice triangolare è nonsingolare se e solo se tutti i suoi minori principali sono non nulli.
Il minore di ordinde k di A in A = LU coincide con il minore di ordine k di U in A(n) ≡ U
Se A è una matrice nonsingolare, la fattorizzazione A = LU esiste se e solo se tutti i minori principali di A sono non nulli.
La fattorizzazione quindi esiste se e solo se U è nonsisingolare, e questo equivale a richiedere che tutti i minori principali di U siano non nulli, e quindi anche tutti quelli di A devono essere non nulli.
Esaminiamo adesso il costo dell’algoritmo di eliminazione di Gauss in termini di occupazione
di memoria.
Strutturalmente, al passo i-esimo l’algoritmo azzera, nella matrice A(1), le componenti
i + 1,...,n della colonna i; al contempo si ottiene l’i-esimo vettore di Gauss che contiene
informazioni soltanto nelle ultime n − i componenti. Possiamo quindi pensare di
sovrascrivere A durante il processo, ottenendo una matrice che contiene la parte
significativa della matrice U nella porzione triangolare superiore e le componenti
significative della matrice L (ovvero gli elementi significativi dei vettori di Gauss) nella
parte strettamente inferiore, tenendo conto che la diagonale della matrice L ha
tutti elementi pari a 1 e non necessita quindi di essere memorizzata esplicitamente.
Possiamo quindi concludere che il metodo di eliminazione di Gauss non richiede
memoria addizionale alla matrice di partenza A, che è quanto di meglio si possa
richiedere.
Per quanto riguarda invece il costo computazionale, ad ogni passo i dell’algoritmo è
necessario calcolare:
Considerando che le prime i componenti del vettore gi sono nulle, che il vettore eiTA(i) corrisponde alla i-esima riga di A(i) che ha le prime i componenti nulle e che sappiamo a priori che le componenti da (i + 1)an della colonna i della matrice A(i+1) sono nulle, si nota che solo la sottomatrice delimitata da (i + 1,i + 1),(n,n) verrà modificata al passo i. Il costo computazionale di una iterazione consiste in n − i divisioni per calcolare il vettore di Gauss, (n − i)2 sottrazioni ed altrettante moltiplicazioni per aggiornare la matrice; in totale la fattorizzazione avrà un costo approssimativo di:
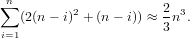 |
Questo codice implementa l’algoritmo di fattorizzazione LU:
Esistono delle classi di matrici per cui è vero che se A è nonsingolare allora lo è anche Ak, ∀k = 1,...n, e sono le matrici a diagonale dominante.
La matrice A ∈ℝn×n si dice a diagonale dominante per righe se:
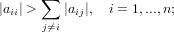 |
e a diagonale dominante per colonne se:
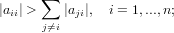 |
Per questa classe di matrici valgono le seguenti proprietà:
Se A è una matrice a diagonale dominante per righe (o per colonne), allora anche tutte le sue sottomatrici principali sono dello stesso tipo
Una matrice A è a diagonale dominante per righe (o per colonne) se e solo se AT è a diagonale dominante per colonne (per righe).
Se una matrice A è diagonale dominante (per righe o per colonne), allora A è non singolare.
Dimostrazione:
Sia A una matrice a diagonale dominante per righe, supponiamo per assurdo che A sia
singolare. Allora deve esistere x≠0 tale che Ax = 0. Assumiamo
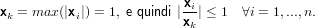 |
Ma se Ax = 0 allora ekTAx = ekT0 = 0, ne consegue che:
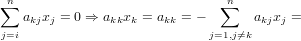 |
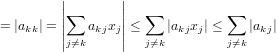 |
ma allora A non è diagonale dominante. Assurdo.
Se A è una matrice a diagonale dominante, allora A è fattorizzabile LU.
Un’altra classe di matrici fattorizzabili LU è quella delle matrici simmetriche e definite positive (sdp).
Una matrice A ∈ℝn×n è sdp se è simmetrica (ovvero A = AT) e se vale:
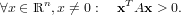 |
Se A è sdp allora aii > 0, ∀i = 1,...,n.
Dimostrazione:
Infati, se A è sdp si dee avere che aii = eiTAei > 0. Cvd.
Se A è sdp allora A è nonsingolare.
Dimostrazione:
Supponiamo per assurdo che A sia contemporaneamente sdp e singolare. Essendo A
singolare deve esistere x≠0 tale che Ax = 0, ovvero xTAx = 0 ovvero A non è sdp.
Cvd.
A è sdp se e solo se ∀k = 1,...,n, Ak è sdp.
Dimostrazione:
Procediamo per assurdo, supponendo Ak non sdp. Allora deve esistere y ∈ℝk,y≠0, tale che
yTAky ≤ 0. Allora deve esistere anche x ∈ℝn tale che x = (y,0..0)T≠0, che soddisfi
0 < xTAx in quanto A è sdp per ipotesi. Ma allora avremmo:
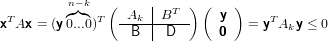 |
che va contro l’ipotesi.
Se A è sdp allora A è fattorizzabile LU
Dimostrazione:
Da quanto dimostrato fino ad ora sappiamo che tutte le sottomatrici principali di A
sono sdp, e quindi anche i corrispondenti minori principali sono tutti non nulli.
Cvd.
Gli elementi diagonali di una matrice simmetrica e definita positiva sono positivi.
Dimostrazione:
Se A è sdp, per definizione si ha che aii = eiTAei > 0.
Una matrice A è sdp se e solo se è scrivibile come:
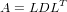 |
dove L è triangolare inferiore a diagonale unitaria e D è diagonale con elementi diagonali
positivi.
Dimostrazione:
Per prima cosa dimostriamo che se A è scrivibile come LDLT allora è sdp. Dobbiamo quindi
dimostrare che ∀x≠0,xTLDLTx > 0. Possiamo considerare il vettore y = LTx e quindi
yT = xTL, sicuramente non nullo in quanto L è una matrice non singolare e x≠0 per ipotesi.
Si può quindi scrivere:
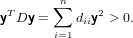 |
Adesso possiamo dimostrare che se A è sdp allora A = LDLT. Abbiamo dimostrato precedentemente che se A è sdp allora è fattorizzabile LU. Possiamo pensare U come DÛ dove:
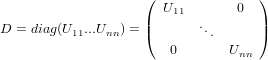 |
ed
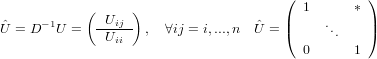 |
ovvero D è una matrice diagonale e Û triangolare superiore a diagonale unitaria. Osserviamo che
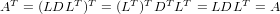 |
e che:
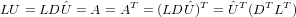 |
ma quindi:
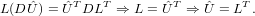 |
Per l’unicità della fattorizzazione LU, in quanto ÛT è triangolare inferiore a diagonale unitaria e DLT è triangolare superiore, si ha che ÛT = L e quindi la fattorizzazione A = LDLT è ben definita. Dimostriamo adesso che gli elementi diagonali di D sono positivi, facendo vedere che questa è sdp. Banalmente D è simmetrica in quanto diagonale, e, qualunque si fissi x≠0 esiste un unico vettore y≠0 che soddisfi LTy = x. Si ha quindi che:
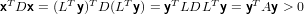 |
in quanto A è sdp.
Trattiamo innanzitutto gli aspetti che riguardano la memorizzazione delle informazioni. Per
quanto riguarda la memorizzazione di matrici strettamente triangolari, dobbiamo pensare di
memorizzare solo la parte che contiene informazioni, evitando di sprecare memoria per la
parte strettamente triangolare nulla. Questo può essere fatto memorizzando la parte
triangolare in un vettore e di utilizzare un piccolo programma che permetta di recuperare
l’elemento ij della matrice triangolare dal relativo vettore. Nel caso quindi della
fattorizzazione LDLT, in quanto stiamo trattando matrici sdp (e quindi triangolari) possiamo
pensare di memorizzarne solo la parte triangolare attraverso il codice appena visto, ed in più
possiamo pensare di riscrivere la matrice di partenza con la porzione strettamente triangolare
di L (o LT) e la diagonale D, mantenendo quindi il costo di memorizzazione inferiore ad n2.
Analizziamo adesso il costo in termidi di operazioni floating-point.
Stiamo lavorando su una matrice A = (aij) = LDLT, una matrice L = (lij che
ha le proprietà di avere lii = 1 ed lij = 0 se j > i e D diagonale. Si ha quindi
che:
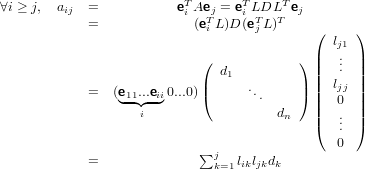 |
e quindi aij = ∑
k=ijlikljkdk, i = j,...,n;j = 1,...,n.
Si posso verificare due casi, i = j e i > j:
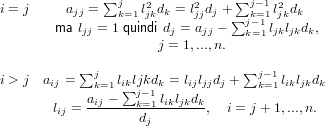 |
Si ha quindi che per effettuare il calcolo della colonna k-esima è necessaria soltanto
l’informazione relativa a quelle precedenti. e che l’elemento aij sia necessario solo per il
calcolo della colonna j-esima; questo ci lascia liberi di sovrascriverlo con le nuove informazioni
derivanti dal calcolo appena effettuato. In particolare possiamo memorizzare le informazioni
relative agli elementi dk sulla diagonale e i fattori lij nella parte strettamente triangolare
inferiore della matrice A. Si deve inoltre tenere conto che ljkdk viene calcolato nel ciclo
esterno e sarà poi necessario nel ciclo interno, è quindi opportuno appoggiarsi ad un
array temporaneo per memorizzare il risultato di questa operazione; a questo scopo
è sufficiente un array di j − 1 locazioni di memoria in quanto l’ultimo elemento
diagonale ad essere calcolato potrà essere memorizzato direttamente sulla matrice
A.
Questo codice implementa l’algoritmo di fattorizzazione LDLT descritto fino ad ora:
Prendiamo adesso in esame il caso in cui la miatrice A che vogliamo fattorizzare sia
nonsingolare ma che non abbia la proprietà di avere tutti i minori principali non nulli.
Abbiamo prima dimostrato che in questo caso la fattorizzazione A = LU non esiste; possiamo
però definire una fattorizzazione che esista sotto la sola ipotesi della nonsingolarità di
A.
Supponiamo di star procedendo al primo passo del metodo di eliminazione di Gauss: per poter
procedere è necessario che a11≠0. Supponiamo però che a11 = 0: in quanto A è
nonsingolare deve esistere, sulla prima colonna, un elemento non nullo. Possiamo quindi
scegliere:
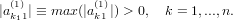 |
Definiamo una matrice elementare di permutazione del tipo:
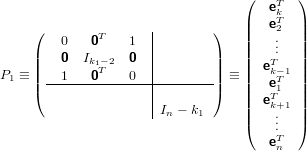 |
e non è altro che la matrice identità di ordine n con le righe 1 e k1 scambiate. Notiamo
che P1 è una matrice simmetrica ed ortogonale, ovvero vale: P1 = P1T = P1−1.
Segue quindi che P1A(1) non è altro che la matrice A(1) con le righe 1 e k1 scambiate.
Adesso abbiamo reso possibile l’effettuazione del primo passo dell’algoritmo di eliminazione di
Gauss, abbiamo infatti reso non nullo a11:
 |
e la prima matrice elementare di Gauss:
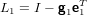 |
che consente quindi di ottenere:
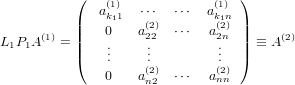 |
É impotante notare che:
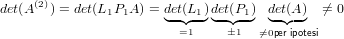 |
Ma A(2) è della forma:
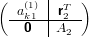 |
e quindi:
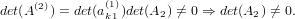 |
Possiamo quindi procedere in modo analogo al metodo di fattorizzazione LU, avendo al passo i-esimo la matrice:
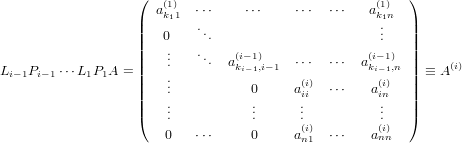 |
Avremo quindi akii(i)≠0 se A è nonsingolare. Definiamo quindi la matrice Pi che permuta le righe i e ki (con ki ≥ i ):
 |
e si avrà quindi che l’elemento (i,i) della matrice PiA(i) diventa akij(i). Definiamo quindi l’i-esimo vettore di Gauss:
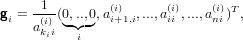 |
e quindi l’i-esima matrice elementare di Gauss:
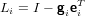 |
tali che:
 |
Con questo procedimento, se A è nonsingolare sarà sempre possibile iterare i passi appena descritti fino a i = n − 1, ottenendo la fattorizzazione:
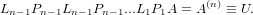 |
Se si tiene conto che le matrici di permutazione elementari Pi sono sia simmetriche che ortogonali e se moltiplicate per un vettore sortiscono l’effetto di permutare le componenti i e ki con ki ≥ i, si può pensare di riscrivere:
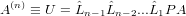 |
dove
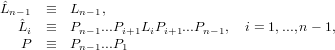 |
P è una matrice di permutazione, ovvero una matrice ortogonale che se moltiplicata per un vettore ne permuta le componenti. Per come abbiamo definito Pi:
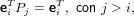 |
e quindi:
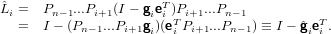 |
Il vettore 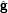 i ha la stessa struttura del vettore elementare di Gauss prima definito ma con le
ultime n−i componenti permutate tra loro. Ne consegue che la struttura della matrice
i ha la stessa struttura del vettore elementare di Gauss prima definito ma con le
ultime n−i componenti permutate tra loro. Ne consegue che la struttura della matrice 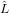 i è
analoga a quella della matrice elementare di Gauss prima definita; si può quindi concludere
che la matrice
i è
analoga a quella della matrice elementare di Gauss prima definita; si può quindi concludere
che la matrice 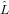 n−1...
n−1...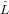 1 ≡ L−1 è triangolare inferiore a matrice unitaria. Abbiamo quindi
ottenuto una fattorizzazione con pivotin parziale:
1 ≡ L−1 è triangolare inferiore a matrice unitaria. Abbiamo quindi
ottenuto una fattorizzazione con pivotin parziale:
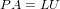 |
Se A è una matrice nonsingolare, allora esiste una matrice di permutazione P tale che PA è
fattorizzabile LU.
Questo metodo permette di estendere l’utilizzo della fattorizzazione LU, infatti si ha che:
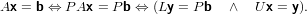 |
e la matrice di permutazione P serve soltanto per permutare il vettore dei termini noti b, operazione che precede direttamente la risoluzione dei sistemi triangiolari sopra descritti nell’ordine specificato.
Questo algoritmo implementa la fattorizzazione LU con pivoting appena descritta:
Studieremo adesso in che modo delle perturbazioni sui dati di un sistema lineare del tipo Ax = b si ripercuotono sulla sua soluzione.
Dobbiamo prima dare delle definizioni:
Sia x ∈ℝn, la norma di un vettore è una funzione definita su uno spazio vettoriale V e codominio in ℝ tale che:
Sia V ∈ℝn. Definiamo:
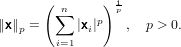 |
Piu in dettaglio:
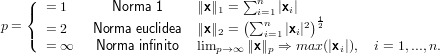 |
Verifichiamo adesso che le norme appena descritte verificano le tre proprietà sopra
elencate.
Per quanto riguarda la prima proprietà si ha che:
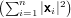
 anche in questo caso abbiamo un sommatoria
di soli valori positivi e vale quanto appena detto per la norma 1.
anche in questo caso abbiamo un sommatoria
di soli valori positivi e vale quanto appena detto per la norma 1.
Per la seconda si ha che:
 = (|α|2 ∑
i=1n|xi|2)
= (|α|2 ∑
i=1n|xi|2) =
|α|(∑
i=1n|xi|2)
=
|α|(∑
i=1n|xi|2) .
.
E infine per la terza:
 ≤ (∑
i=1n|xi| + ∑
i=1n|yi|)
≤ (∑
i=1n|xi| + ∑
i=1n|yi|) in
quanto vale la disuguaglianza triangolare per i valori assoluti.
in
quanto vale la disuguaglianza triangolare per i valori assoluti.
Notiamo inoltre che le norme sono tra loro equivalenti, vale infatti che:
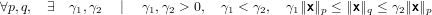 |
Sia V = ℝm×n e A ∈ℝm×n. Definiamo la norma “p” su una matrice indotta dalla corrispondente norma “p” su vettore come:
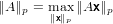 |
dove ∥A∥ e ∥x∥ possono essere su spazi diversi se A è rettangolare.
Andiamo a studiare il sistema lineare:
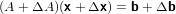 |
dove le perturbazioni ΔA e Δb determinano la perturbazione Δx sulla soluzione. Consideriamo, per semplicità, il caso in cui i dati dipendano da un parametro scalare di perturbazione di dimensioni prossime a zero:
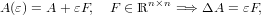 |
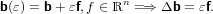 |
Da cui consegue:
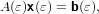 |
Si osservi che:
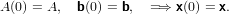 |
Sviluppando in serie di Taylor in ε = 0, si ottiene:
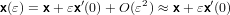 |
cioè
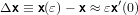 |
Si può inoltre ricavare che:
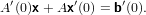 |
Quindi:
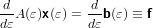 |
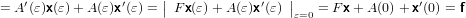 |
che permette di ottenere:
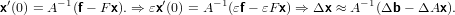 |
Passando alle norme:
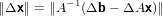 |
Ma per la disugualianza triangolare si può affermare che:
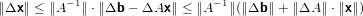 |
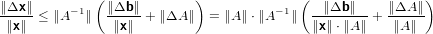 |
ma tenendo condo che:
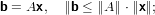 |
si può concludere che:
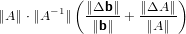 |
e quindi:
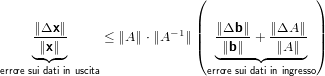 |
Abbiamo ottenuto una equazione che misura una sorta di errore relativo sul risultato, ed in particolare abbiamo che k = ∥A∥⋅∥A−1∥è il numero di condizionamento del problema. É importante notare che k(A) = ∥A∥⋅∥A−1∥≥∥A ⋅ A−1∥ = ∥I∥ = 1.
Poniamo adesso il caso di voler risolvere un sistema di equazioni lineari in cui ci siano più equazioni che incognite ma in cui la matrice dei coefficienti abbia rango massimo. Formalmente siamo quindi nel caso:
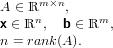 |
In particolare possiamo considerare la matrice A in questo modo:
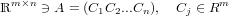 |
si ha che:
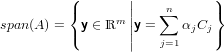 |
dove
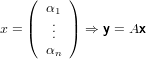 |
ed
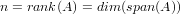 |
Possiamo quindi affermare che:
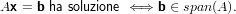 |
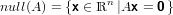 |
Se la matrice ha rango massimo null(A) contiene un solo vettore; generalmente si ha:
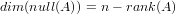 |
se il rango della matrice non è massimo.
In particolare avremo che:
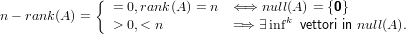 |
Dobbiamo notare che:
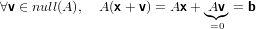 |
ovvero se rank(A) non è massimo ci sono infinite soluzioni.
Sia b ∈ℝm un vettore e span(A) = n < m il rango della matrice. Allora si ha
che span(A) ⊊ ℝm. Questo significa che l’insieme differenza (ℝm − span(A)) è
molto grande e la situazione b ∈ span(A) risulta essere un evento piu “fortunato”
che probabile, ovvero in generale non si può assumere che b sia nello spazio di A.
Per risolvere il sistema sopra descritto proveremo dunque a trovare il vettore x che minimizza il vettore:
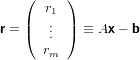 |
Ovvero andremo a cercare la suluzione del sistema nel senso dei minimi quadrati:
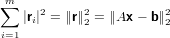 |
Se A è una matrice in ℝm×n,m > n,rank(A) = n allora esistono Q ∈ℝm×m,QTQ = Im e
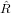 ∈ℝn×n triangolare superiore e nonsingolare tali che:
∈ℝn×n triangolare superiore e nonsingolare tali che:
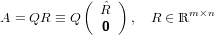 |
É importante ricordare la seguente proprietà delle matrici ortogonali:
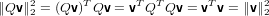 |
ovvero la norma euclidea è invariante per moltiplicazioni per matrici ortogonali a sinistra o a
destra.
Vediamo su quali fattori lavorare per minimizzare il vettore residuo:
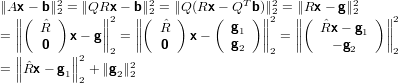 |
in cui abbiamo definito e quindi utilizzato:
 |
Generalmente quindi b non appartiene allo span(A). Ne deriva quindi che se 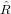 x = g1 allora
∥Ax −b∥22 = ∥g2∥22 ≡ min. É importante osservare che:
x = g1 allora
∥Ax −b∥22 = ∥g2∥22 ≡ min. É importante osservare che:
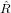 x = g1 ammette una unica soluzione in quanto
x = g1 ammette una unica soluzione in quanto 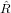 è non
singolare, e questa è quindi la soluzione ai minimi quadrati di Ax = b;
è non
singolare, e questa è quindi la soluzione ai minimi quadrati di Ax = b;
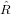 è triangolare superiore e il sistema è quindi facilmente risolvibile;
è triangolare superiore e il sistema è quindi facilmente risolvibile;
Dato il vettore:
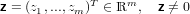 |
vogliamo determinare una matrice ortogonale H tale che:
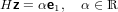 |
Si ha che:
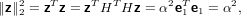 |
ovvero possiamo definire α come:
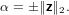 |
Consideriamo quindi una matrice della seguente forma:
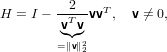 |
dove v ∈ℝm sarà diverso dal vettore nullo se anche z lo è. La matrice H così costruita è simmetrica per definizione, ed è anche ortogonale:
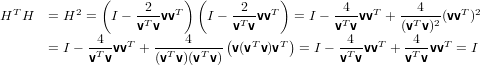 |
Scegliamo adesso un vettore
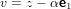 |
e verifichiamo se Hz = αe1, α ∈ℝ.
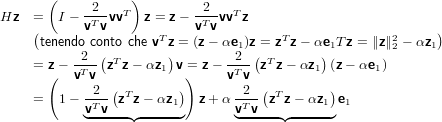 |
Dall’equazione sopra scritta notiamo che se gli scalari sopra evidenziati fossero di valore pari ad 1 allora otterremmo Hz = αei, dimostriamolo:
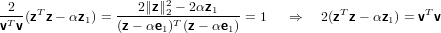 |
dove svolgendo vTv otteniamo
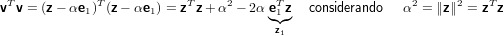 |
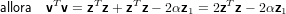 |
per cui abbiamo verificato
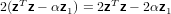 |
abbiamo quindi dimostrato che Hz = αe1.
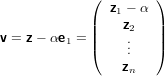 |
tenendo conto del condizionamento della somma algebrica imponiamo:
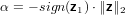 |
Il calcolo di v avrà pertanto numero di condizionamento pari a uno.
Vediamo adesso come si possa risparmiare una locazione di memoria nella memorizzazione di
v:
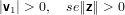 |
possiamo quindi riscrivere v come:
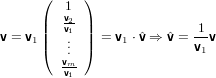 |
Notiamo adesso che:
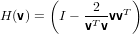 |
e quindi
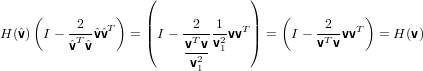 |
ovvero si può sostituire il vettore v con un qualunque altro vettore multiplo scalare di esso e la matrice di Householder non cambia. Possiamo quindi usare il vettore normalizzato e risparmiare una locazione di memoria.
Dimostriamo adesso in maniera costruttiva l’esistenza della fattorizzazione QR:
Sia:
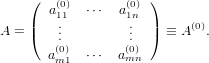 |
dove l’indice superiore indica il passo più recente in cui è stato modoficato l’elemento
corrispondente.
Considerando la prima colonna della matrice A(0) possiamo definire la matrice di Householder
H1 ∈ℝm×m tale che:
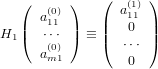 |
e se A ha rango massimo si deve necessariamente avere che a11(1)≠0, altrimenti la prima colonne della matrice risulterebbe nulla. Otterremo quindi:
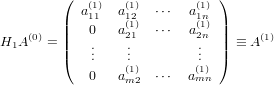 |
Possiamo adesso iterare il passo fatto in precedenza sulla seconda colonna della matrice A(1) a partire dalla seconda componente e definire quindi una matrice di Householder in questo modo:
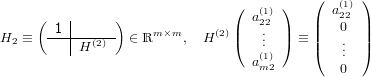 |
La seconda matrice di Householder così ottenuta è quindi la composizione della matrice identità con una sottomatrice di Householder di dimensione m − 1. Notiamo che essa è ancora ortogonale e vale:
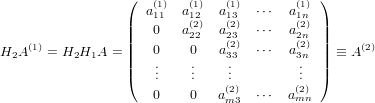 |
Anche a questo passo si dovrà avere che a22(2)≠0 se la matrice A ha rango massimo.
Generalizzando al passo i-esimo si avrà quindi:
 |
con ajj(j)≠0, j = 1,...,i.
Possiamo quindi definire la matrice di Householder al passo i + 1 come:
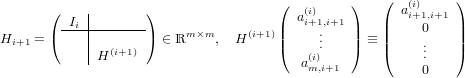 |
ottenendo così ancora una matrice ortogonale che soddisfa:
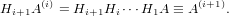 |
con ai+1,i+1(i+1)≠0. Procedento in questo modo dopo n passi si arriva alla matrice:
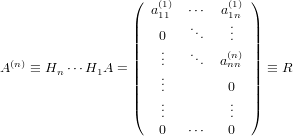 |
con aii(i)≠0, i = 1,...,n. Se poniamo quindi QT = Hn H1, abbiamo ottenuto la
fattorizzazione A = QR.
H1, abbiamo ottenuto la
fattorizzazione A = QR.
| Flops | Memoria | |
| LU | O( n3) n3) | n2 |
| LDL | O(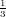 n3) n3) | 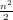 + O(n) + O(n) |
| PLU |  n3 n3 | n2 + O(n) |
| QR | O( n2(3m − n)) n2(3m − n)) | O(m ∗ n) |
![f : [a,b] ⊂ ℝ → ℝ](relazione304x.png) |
Questo può rendersi necessario per diversi motivi:
Avendo a disposizione i seguenti dati:
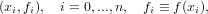 |
ricerchamo un polinomio interpolante la f(x) sulle ascisse xi ∈ [a,b], xi < xj se i < j,xi≠xj se i≠j, tale che:
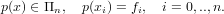 |
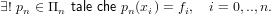 |
Dimostrazione:
Un generico polinomio di grado n sarà nella forma:
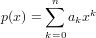 |
che descrive il sistema di equazioni lineari:
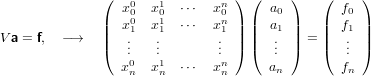 |
in cui V è una matrice di Vandermonde trasposta univocamente definita dalle ascisse xi. Il determinante di tale matrice vale:
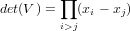 |
In quanto per ipotesi le ascisse sono tra loro distinte, abbiamo che V è nonsingolare e quindi esiste ed è unica la soluzione del sistema lineare, ovvero esiste ed è unico il polinomio suddetto. Non utilizzeremo però questa matrice per determinare in polinomio, in quanto tra le altre cose sappiamo anche che essa diviene molto mal condizionata al crescere di n.
Per ottenere un problema discreto con proprietà piu favorevoli rispetto a quello V a = f sopra
descritto, si può pensare di utilizzare basi diverse per Πn.
Ad esempio la base di Lagrange:
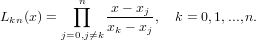 |
I polinomi appena descritti sono tutti ben definiti in quanto, per ipotesi, xi≠xj con i≠j.
Dati i polinomi di Lagrange appena descritti definiti sulle ascisse a ≤ x0 < x1 < ... < xn ≤ b:
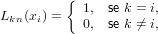 |
inoltre:
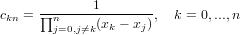 |
Il polinomio
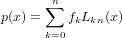 |
appartiene a Πn e soddisfa i vincoli di interpolazione p(xi) = fi, i = 0,1,...,n.
Dimostrazione:
p(x) ∈ Πn in quanto per definizione produttoria di n termini di grado 1; inoltre si ha
che:
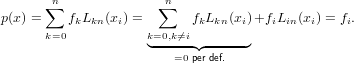 |
La base di Lagrange genera una forma del polinomio interpolante in cui i coefficienti sono facili da calcolare; questa rappresentazione però si presta male alla computazione in quanto non consente di generare il polinomio in maniera incrementale ma, dovendo calcolare e poi sommare k polinomi di grado n, ha un costo computazionale molto elevato.
Indichiamo con pr(x) il polinomio in Πr che interseca la funzione da approssimare sulle ascisse x0,x1,...,xr che supponiamo noto, possiamo definire il successivo pr+1(x) a partire da questo, e questo può essere fatto in modo semplice utilizzando la base di Newton così definita:
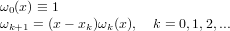 |
che gode delle seguenti proprietà:
 |
La famiglia di polinomi interpolanti pr(x)r=0n tali che:
si genera ricorsivamente in questo modo:
![p0(x) = f0ω0(x)
pr(x) = pr−1(x)+ f[x0,x1,...,xr]ωr(x), r = 1,..,n.](relazione318x.png) | (4.1) |
dove:
![r
f[x ,x ,...,x ] = ∑ ∏------fk-------.
0 1 r k=0 rj=0,j⁄=k(xk − xj)](relazione319x.png) | (4.2) |
e la quantità f[x0,x1,...,xr] è detta differenza divisa di ordine r della funzione f(x) sulle
ascisse x0,x1,...,xr.
Dimostrazione:
Ragionando per induzione, la tesi è banalmente vera per r = 0. Supponendola quindi vera per
r − 1 vogliamo dimostrare che è vera anche per r:
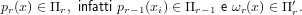 |
Inoltre per i < r si ha:
![pr(xi) = pr−1(xi)+ f[x0,x1,...,xr]ωr(xi) = pr−1(xi) = fi](relazione321x.png) |
in quanto ωr(xi) = 0 e per l’ipotesi di induzione. Se i = r:
![p(x ) = p (x )+ f[x,x ,...,x]ω (x ) = f
r r r−1 r 0 1 r r r r](relazione322x.png) |
e quindi
![f[x0,x1,...,xr] = fr −-pr−-1(xr).
ωr(xr)](relazione323x.png) |
L’espressione è ben definita in quanto, essendo le ascisse distinte, ωr(xr)≠0. Verifichiamo
adesso che l’espressione appena ottenuta è formalmente uguale a quella (4.2):
esprimendo il polinomio pr(x) secondo la base di Lagrange:
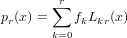 |
Per l’unicità del polinomio interpolante questi polinomi devono conicidere con quelli in (4.1). I
loro coefficienti principali devono quindi a loro volta conicidere.
Considerando la natura iterativa della forma di Newton si ottiene l’espressione:
![n
p(x) ≡ p (x) = ∑ f[x ,...,x ]ω (x).
n r=0 0 r r](relazione325x.png) |
Il denominatore di Lkn(x) è dato da ω′n+1(xk), mentre quello di f[x0,x1,...,xr] è ω′r+1(xk)
Le differenze divise di f(x) sulle ascisse a ≤ x0 < x1 < ... < xn ≤ b definisco i
coefficienti della rappresentazione del polinomio interpolante p(xi) rispetto alla base di
Newton.
Le differenze divise di f(x) sulle ascisse a ≤ x0 < x1 < ... < xn ≤ b godono delle seguenti
proprietà:
![(α ⋅f +β ⋅g)[x0,...,xr])α⋅f[x0,...,xr]+ β ⋅g[x0,...,xr];](relazione326x.png) |
![f[xi0,...,xir] = f [x0,...,xr];](relazione327x.png) |
![{
ak, se r = k,
f[x0,x1,...,xr] = 0, se r > k;](relazione328x.png) |
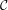 (r), allora:
(r), allora:
![(r)
f[x0,x1,...,xr] = f-(ε), ε ∈ [min xi,max xi];
r! i i](relazione329x.png) |
![f[x1,...,xr]− f[x0,...,xr−1]
f[x0,x1,...,xr−1,xr] =---------xr −-x0-------](relazione330x.png) |
Dal punto quattro consegue che se le ascisse coincidono (x0 = ... = xn), il polinomio
pn(x) = ∑
r=0nf[x0,...,xr]ωr(x) diventa il polinomio di Taylor di f(x) di punto iniziale
x0.
La proprietà descritta nel punto cinque è invece molto interessante dal punto di vista
algoritmico: spiega infatti come sia possibile costruire una differenza divisa di ordine r a
partire da due differenze divise di ordine r − 1 che differiscono solo per una delle ascisse.
Tenendo conto che f[xi] = fi, i = 0,1,...,n, siamo in grado di generare la seguente tabella
triangolare, in cui la diagonale principale contiene i coefficienti del polinomio interpolante
nella forma di Newton:
| 0 | 1 | 2 |  | n − 1 | n | |
| x0 | f[x0] | |||||
| x1 | f[x1] | f[x0,x1] | ||||
 |  | f[x1,x2] | f[x0,x1,x2] | |||
 |  |  |  | 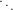 | ||
| xn−1 | f[xn−1] | f[xn−2,xn−1] |  | f[x0,...,xn−1] | ||
| xn | f[xn] | f[xn−1,xn] | f[xn−2,xn−1,xn] |  | f[x1,...,xn] | f[x0,...,xn] |
Notiamo che le colonne della tabella vanno calcolate da sinistra verso destra; possiamo però calcolare ciascuna colonna dal basso verso l’alto: in questo modo gli elementi adiacenti a sinistra non sono più necessari nel seguito e si posso quindi riscrivere con il nuovo elemento appena calcolato.
Questo codice implementa il calcolo delle differenze divise appena descritto:
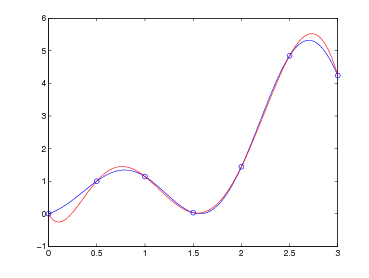
Consideriamo le seguenti ascisse di interpolazione:
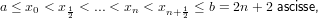 |
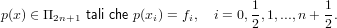 |
Se facciamo in modo che:
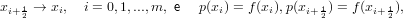 |
si ha che:
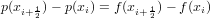 |
e dividendo membro a membro per xi+ − xi si ottiene:
− xi si ottiene:
![′ ′
p[xi,xi+ 12] = f[xi,xi+12] ⇒ p(xi) = f(xi)](relazione347x.png) |
Come conseguenza abbiamo qundi che il polinomio p(x) è ancora definito e soddisfa i vincoli di interpolazione:
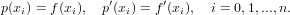 |
Abbiamo appena definito il polinomio interpolante di Hermite.
Passando al polinomio di Taylor, considerando di avere una sola ascissa:
![′
p(x)) = f[x0]+ f[x0,x0](x− x0) ≡ f(x0) +f (x0)(x − x0)](relazione349x.png) |
Per generalizzare, se si considerano le ascisse in questo modo:
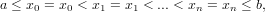 |
il polinomio di Hermite sarà dato da:
![p(x) = f [x0]+ f[x0,x0](x− x0)+ f[x0,x0,x1](x − x0)2+
f [x0,x0,x1,x1](x− x0)2(x − x1)+
f [x0,x0,x1,x1,x2](x − x0)2(x − x1)2 + ⋅⋅⋅+
f [x0,x0,x1,x1,...,xm,xm ](x− x0)2⋅⋅⋅(x − xm−1)2(x− xm ).](relazione351x.png) |
Per calcolare i coefficienti ci serviremo dell’algoritmo implementato qui di seguito, che non è altro che una modifica all’algoritmo per il calcolo delle differenze divise. In questo algoritmo avrà in ingresso un vettore f contenente i valori:
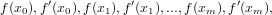 |
ed un vettore x contenente le ascisse.
Questo codice implementa il calcolo delle differenze divise appena descritto:
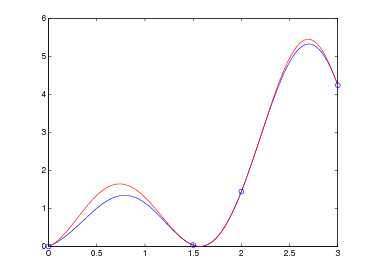
Sia p(x) ∈ Πn il polinomio interpolante tale che, note le coppie (xi,fi), p(xi) = fi con i = 0,1,...,n. Possiamo definire l’errore di interpolazione come:
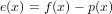 |
dove e(x) è l’errore che si commette nell’approssimare f(x) mediante il suo polinomio interpolante p(x). Segue naturalmente che, per definizione, e(xi) = 0, i = 0,1,...,n, ma è di nostro interesse misurare questa funzione quando x non appartiene a x0,...,xn.
Sia
![n
p(x) = ∑ f[x ,...,x ]ω (x),
r=0 0 r r](relazione355x.png) |
tale da soddisfare i vincoli di interpolazione p(xi) = fi con i = 0,1,...,n. Il suo errore di interpolazione è:
![e(x) = f [x0,x1,...,xn,x]ωn+1(x).](relazione356x.png) |
Dimostrazione:
Si consideri un generico punto per semplicità distinto dalle ascisse di interpolazione
x0,...,xn, ed il polinomio (x) ∈ Πn+1 che soddisfi sia gli stessi vincoli di interpolazione di
p(x) che:
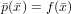 |
Dal teorema sulla forma di Newton segue:
![¯p(¯x) = p(¯x)+ f[x ,x ,...,x ,¯x]ω (¯x).
0 1 m n+1](relazione358x.png) |
Tenendo conto del vincolo aggiunto e della genericità del punto :
![f(¯x)− p(¯x) = f[x ,x ,...,x ,¯x]ω (¯x),
0 1 m n+1](relazione359x.png) |
e quindi abbiamo appena ottenuto la tesi. Cvd.
Se la funzione f(x) ∈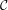 (n+1), allora:
(n+1), allora:
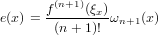 |
con ξ ∈ [min{x0,x},max{xn,x}].
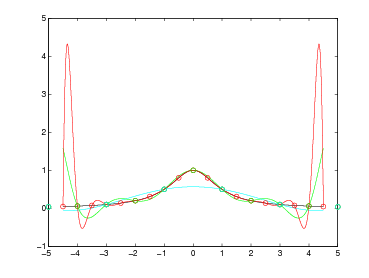
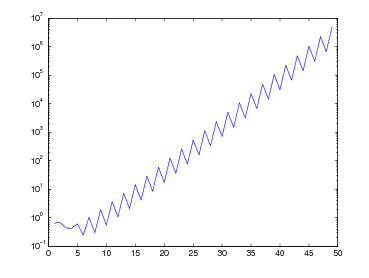
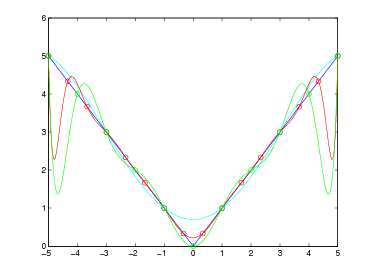
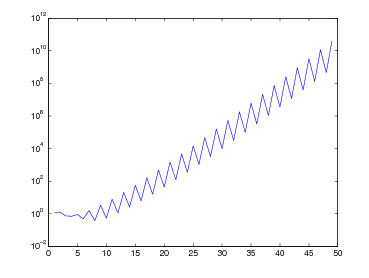
Dalla struttura dell’errore di interpolazione si capisce che questo è fondamentalmente guidato
da due componenti:
Si ha pertanto che ωn+1(x) oscilla quando x ∈ [x0,xn] e si annulla nelle ascisse di interpolazione; ma |ωn+1(x)| cresce quanto |xn+1| se x < x0 o x > xn. Si può concludere quindi che generalmente p(x) può essere utilizzato in maniera utile per approssimare la funzione di partenza f(x) solo all’interno del range [x0,xn].
Per effettuare lo studio del condizionamento del problema occorre per prima cosa identificare quali siano i dati in ingresso per i quali una perturbazione di questi si rifletta sul risultato finale. Per definire il polinomio p(x) ci siamo serviti di un insieme di coppie di numeri (fi,xi), delle quali, in generale, possiamo dire che:
Possiamo quindi considerare l’insieme dei valori delle ascisse come parametri fissati del problema,
e quindi considerare le ordinate gli unici dati in ingresso soggetti ad errore. Consideriamo la
funzione 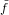 (x) una perturbazione di f(x), e indicheremo con
(x) una perturbazione di f(x), e indicheremo con 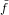 i le valutazioni di
i le valutazioni di 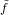 (xi) come
già fatto in precedenza con la f(x). Definiamo adesso, espressi nella forma di Lagrange, i due
polinomi:
(xi) come
già fatto in precedenza con la f(x). Definiamo adesso, espressi nella forma di Lagrange, i due
polinomi:
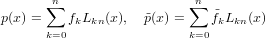 |
che sono rispettivamente il polinomio costruito a partire dai dati esatti e quello invece costruito sui dati perturbati. Confrontandoli si ottiene:
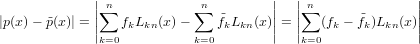 |
e per disugualianza triangolare possiamo affermare:
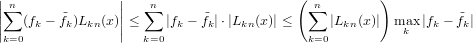 |
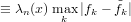 |
dove λn(x) è detta funzione di Lebesgue. Per come è stata definita, λn(x) dipende solo dalla scelta delle ascisse di interpolazione. Definiamo adesso:
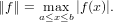 |
Abbiamo quindi che:
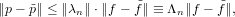 |
dove Λn è detta costante di Lebesgue, e dipende soltanto dalla scelta dell’intervallo [a,b]
considerato e dalla scelta delle ascisse di interpolazione all’interno di questo.
Abbiamo ottenuto che ∥f −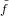 ∥è una misura dell’errore sui dati in ingresso, mentre ∥p −
∥è una misura dell’errore sui dati in ingresso, mentre ∥p −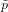 ∥
misura l’errore sul risultato. La costante di Lebesgue appena definita misura pertanto
l’amplificazione massima sul risultato dell’errore dei dati in ingresso, e definisce quindi il
numero di condizionamento del problema. É utile ricordare che Λn ≥ O(log n) per n →∞,
ovvero il problema diviene sempre più malcondizionato al crescere di n. Inoltre la scelta di
ascisse equidistanti genera una successione {Λn} che diverge in modo esponenziale al crescere
di n; ne consegue che questo metodo non è una scelta molto arguta se si vogliono usare valori
molto elevati per n.
∥
misura l’errore sul risultato. La costante di Lebesgue appena definita misura pertanto
l’amplificazione massima sul risultato dell’errore dei dati in ingresso, e definisce quindi il
numero di condizionamento del problema. É utile ricordare che Λn ≥ O(log n) per n →∞,
ovvero il problema diviene sempre più malcondizionato al crescere di n. Inoltre la scelta di
ascisse equidistanti genera una successione {Λn} che diverge in modo esponenziale al crescere
di n; ne consegue che questo metodo non è una scelta molto arguta se si vogliono usare valori
molto elevati per n.
Vediamo adesso come l’errore di interpolazione ed il condizionamento del problema siano
strettamente interconnessi:
Sia f(x) una funzione continua in [a,b], allora esiste p∗(x) ∈ Πn tale che:
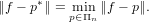 |
Questo polinomio è detto “polinomio di miglior approssimazione di grado n di f(x) sull’intervallo [a,b]”.
Sia p∗(x) il polinomio di migliore approssimazione di grado n di f(x). Allora si ha che:
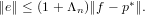 |
Dimostrazione:
considerando che p∗(x) ∈ Πn coincide con il proprio polinomio interpolante sulle ascisse
a ≤ x0 < ... < xn ≤ b, si ha:
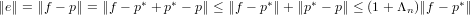 |
come volevasi dimostrare.
Come conseguenza, non è detto che l’errore diminuisca al crescere di n se la costante di
Lebesgue cresce esponenzialmente. Per precisare, introduciamo il “modulo di continuità di
una funzione” relativo all’intervallo [a,b]:
![ω(f;h) ≡ sup{|f(x)− f(y)| : x,y ∈ [a,b],|x− y| ≤ h}](relazione379x.png) |
dove h > 0 è un parametro assegnato. Possiamo osservare che se f(x) ∈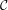 (1), allora
ω(f;h) → 0 se anche h → 0,e che se f(x) è Lipschitziana con costante L, allora
ω(f;h) ≤ Lh.
(1), allora
ω(f;h) → 0 se anche h → 0,e che se f(x) è Lipschitziana con costante L, allora
ω(f;h) ≤ Lh.
Il polinomio di approssimazione di una funzione p(x) = minp∈Πn∥f −p∥,f(x) ∈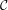 (0), è tale
che:
(0), è tale
che:
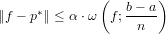 |
in cui la costante α è indipendente da n. Possiamo quindi concluedere che, per una funzione generica vale:
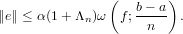 |
Trattiamo adesso la risoluzione del seguente problema:
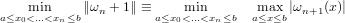 |
che deriva dallo studio del condizionamento del problema, in cui ci si accorge che una scelta oculata delle ascisse di interpolazione deve essere fatta tenedo conto che:
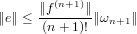 |
dove il fattore 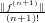 è indipendente dalla scelta delle ascisse di interpolazione.
è indipendente dalla scelta delle ascisse di interpolazione.
Per semplicità, assumiamo che:
![[a,b] ≡ [− 1,1]](relazione385x.png) |
In questo modo non si perde in generalità, infatti è sempre possibile costruire una corrispondenza biunivoca tra gli insiemi Z = {z : z ∈ [−1,1]} e Y = {y : y ∈ [a,b]}. Si ha che:
![( a+ b b− a )
y ≡ --2--+ -2--z ∈ [a,b]](relazione386x.png) |
infatti se z = −1, y = a e se z = 1, y = b; per tutti i valori di z compresi tra −1 ed 1 si
ha che alla quantità 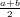 (che indica la metà esatta dell’intervallo [a,b]) viene sommata una
quantità −
(che indica la metà esatta dell’intervallo [a,b]) viene sommata una
quantità −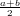 ≤
≤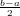 z ≤
z ≤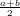 e quindi tutti i valori risultanti devono appartenere
all’intervallo [a,b].
e quindi tutti i valori risultanti devono appartenere
all’intervallo [a,b].
Viceversa, si ha che:
![2y−-a-−-b
z ≡ b− a ∈ [− 1,1]](relazione391x.png) |
infatti se y = a, z = −1 e se y = b, z = 1; per tutti i valori di y compresi tra a e b si ha
che |2y −a−b|≤|b−a| e quindi tutti i valori risultanti appartengono all’intervallo [−1,1].
Possiamo adesso definirela famiglia di polinomi di Chebyshev di prima specie come:
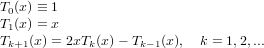 |
Valgono le seguenti proprietà:
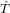 k,, in cui
k,, in cui
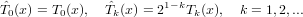 |
è una famiglia di polinomi monici di grado k, k = 1,2,....
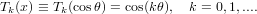 |
Gli zeri di Tk(x), tra loro distinti, sono dati da:
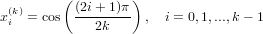 |
Per x ∈ [−1,1], i valori estremi di Tk(x) sono assunti nei punti:
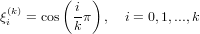 |
e corrispondono a:
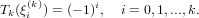 |
Si ha quindi che ∥Tk∥ = 1, e ∥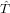 k∥ = ∥21−kTk∥ = 1. Inoltre per k = 1,2,...:
k∥ = ∥21−kTk∥ = 1. Inoltre per k = 1,2,...:
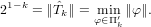 |
Segue quindi che, sulle ascisse di interpolazione a ≤ x0 < ...axn ≤ b per l’intervallo [−1,1,] scelte in questo modo:
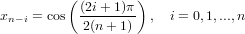 |
si ottiene:
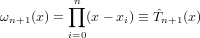 |
che è la soluzione del problema che ci eravamo posti. Con questa scelta delle ascisse, se la funzione è sufficientemente regolare si ottiene che:
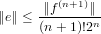 |
Si ha quindi che la corrispondente costante di Lebesgue vale:
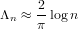 |
che risulta quindi avere una cresctia ottimale anche per un numero di ascisse tendente all’infinito.
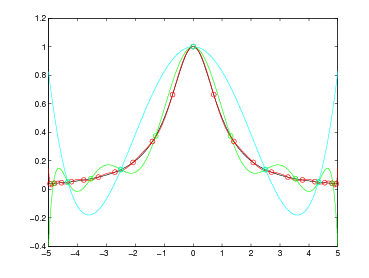
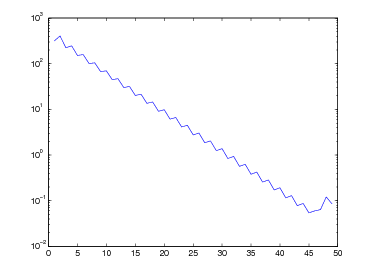
Abbiamo appena visto come al crescere del grado del polinomio interpolante sia necessario
effettuare una scelta delle ascisse di interpolazione che non faccia crescere in maniera
importante la costante di Lebesgue; d’altro canto se si mantiene basso il numero
n delle ascisse di interpolazione il modulo di continuità di f, ω = 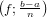 non
può tenedere a zero una volta fissato l’intervallo [a,b]. Possiamo però fissare una
partizione dell’intervallo originario Δ = {a = x0 < x1 < ... < xn = b}, per la quale
h = maxi=1,...,n(xi − xi−1) tende a zero se n tende all’infinito, e considerare, per ogni
sottointervallo [xi−1,xi] della partizione, un polinomio di grado m fissato interpolante f negli
estremi del sottointervallo. In questo modo si ha che il problema del condizionamento
perde importanza in quanto m rimane costante (e quindi anche l’errore), mentre a
questo punto vale che ω(f;h) tende a zero per n che tende all’infinito. Quella
che abbiamo appena descritto è una funzione polinomiale a tratti, definiamola più
esattamente:
non
può tenedere a zero una volta fissato l’intervallo [a,b]. Possiamo però fissare una
partizione dell’intervallo originario Δ = {a = x0 < x1 < ... < xn = b}, per la quale
h = maxi=1,...,n(xi − xi−1) tende a zero se n tende all’infinito, e considerare, per ogni
sottointervallo [xi−1,xi] della partizione, un polinomio di grado m fissato interpolante f negli
estremi del sottointervallo. In questo modo si ha che il problema del condizionamento
perde importanza in quanto m rimane costante (e quindi anche l’errore), mentre a
questo punto vale che ω(f;h) tende a zero per n che tende all’infinito. Quella
che abbiamo appena descritto è una funzione polinomiale a tratti, definiamola più
esattamente:
sm(x) è una spline di grado m sulla partizione Δ se:
 ∈ Πm](relazione408x.png) , i = 1,...,n.
, i = 1,...,n.Se si aggiunge la condizione:
 |
allora la spline è quella interpolante la funzione f(x) nei nodi della partizione Δ.
Se sm(x) è una spline di grado m sulla partizione Δ = {a = x0 < x1 < ... < xn = b}, allora
sm′(x) è una spline di grado m − 1 sulla stessa partizione.
Dimostrazione:
Se sm(x) ∈ℂ(m−1), allora sm′(x) ∈ℂ(m−2) e se sm|[xi−1,xi](x) ≡ pi(x) ∈ Πm, allora
p′(x) ∈ Πm−1.
L’insieme delle funzioni spline di grado m definite sulla partizione Δ è uno spazio vettoriale di dimensione m + n.
Ne consegue quindi che sono necessarie m + n condizioni indipendenti per individuare univocamente la spline interpolante una funzione su una partizione assegnata (m + n− 1 se si considera n l’esatto numero di punti di interpolazione); in quanto tipicamente abbiamo in totale n + 1 condizioni di interpolazione (le coppie (xi,fi)), queste permettono l’individuazione unica della spline lineare, che coincide con la spezzata congiungente i punti {(xi,fi)}i=0,...,n in questo modo:
 = -----i−-1-i----i-----i−1-, i = 1,...,n.
xi − xi−1](relazione410x.png) |
Per identificare una spline di ordine più elevato è necessaria l’imposizione di oppurtune condizioni aggiuntive.
Come detto prima, per ottenere una spline cubica occorre imporre, oltre alle n + 1 condizioni di interpolazione, due condizioni aggiuntive, dalla cui scelta si ottengono spline cubiche differenti.
Questa scelta consiste nell’imporre:
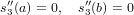 |
In questo caso supponiamo di conoscere i valori di f′(x) negli estremi della partizione, e quindi imponiamo:
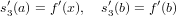 |
Se la funzione che stiamo interpolando è periodica e l’intervallo [a,b] contiene un numero finito e intero di periodi, si possono imporre le condizioni:
 |
In questo caso imponiamo che uno stesso polinomio in Π3 costituisca la restrizione della spline sull’intervallo [x0,x1] ∪ [x1,x2], ed un’altro polinomio analogo faccia lo stesso su [xn−1,xn−1] ∪ [xn−1,xn]. Le condizioni da imporre saranno quindi:
 = s′′3′ |[x1,x2](x1), s′3′′|[xn−1,xn−1](xn −1) = s′′3′ |[xn−1,xn](xn−1)](relazione414x.png) |
Se si osserva che s3′′′|[xi−1,xi](x) ∈ Π0, si può esprimere le condizioni suddette come:
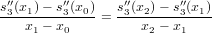 |
e
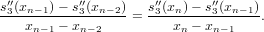 |
Andiamo adesso ad approssimare una funzione f(x) definita su un’intervallo [a,b] con una spline cubica, prendendo in esame una partizione dell’intervallo Δ = {a = x0 < ... < xn = b}. Osserviamo come se s3(x) è una spline cubica, allora s3′(x) è una spline quadratica e s3′′(x) una lineare. Vale quindi che:
 = hi , x ∈ [xi−1,xi]](relazione417x.png) |
dove:
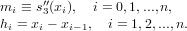 |
Integrando questa equazione si ottiene :
 =------------2h------------ + qi, x ∈ [xi−1,xi]
i](relazione419x.png) |
dove qi è una costante di integrazione, e integrando ancora una volta si ottiene:
 = 6hi + qi(x− xi−1)+ ri, x ∈ [xi− 1,xi]](relazione420x.png) |
dove ri è una costante di integrazione. Imponiamo adesso i vincoli di interpolazione, ovvero che s3(xi) = fi, i = 0,1,...,n, per ricavare ri e qi:
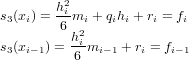 |
da cui:
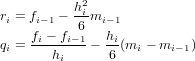 |
Abbiamo quindi che :
 = (x−-xi−1)-mi +-(xi −-x)-mi−1 + fi −-fi−1-− hi(mi − mi −1),
2hi hi 6](relazione423x.png) |
sempre con x ∈ [xi−1,xi]. Imponiamo adesso la continuità di s3′(x), tenendo conto che:
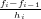 = f[xi−1,xi]
= f[xi−1,xi]quindi:
 = s′3|[xi,xi+1](xi)
hi hi hi+1- hi+1
2 mi − 6 (mi − mi−1)+ f[xi−1,xi] = − 2 mi + f[xi,xi+1]− 6 (mi+1 − mi )
himi −1 + mi(2hi + 2hi+1)+ hi+1mi+1 = 6(f[xi,xi+1]− f[xi−1,xi])](relazione425x.png) |
e dividendo membro a membro per hi + hi+1(= xi+1 − xi−1):
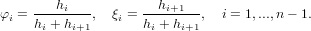 |
e quindi:
![φ m + 2m + ξmi + 1 = 6f [x ,x,x ], i = 1,...,n− 1.
i i−1 i i i−1 i i+1](relazione427x.png) |
Si osserva che φi,ξi > 0 e φi + ξi = 1 per i = 1,...,n − 1.
Poniamoci adesso nel caso delle spline naturali, e imponiamo quidni la condizione
m0 = mn = 0. Si ottiene immediatamente il sistema:
![( ) ( ) ( )
2 ξ1 m1 f[x0,x1,x2]
|| φ2 2 ξ2 || || m2 || || f[x1,x2,x3] ||
|| ... ... ... || || ... || = 6|| ... ||
|| . . || || . || || . ||
( .. .. ξn−2 ) ( .. ) ( .. )
φn−1 2 mn −1 f[xn−2,xn− 1,xn]](relazione428x.png) |
Notiamo come questa matrice goda di diverse proprietà:
Andiamo adesso ad imporre le condizioni not-a-knot:
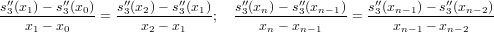 |
che significa porre:
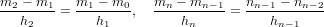 |
da cui si ricava:
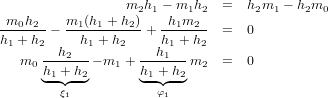 |
in modo analogo si ricava che:
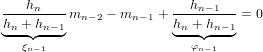 |
che da origine alla matrice:
![( ) ( ) ( 0 )
ξ1 − 1 φ1 m0 | f [x0,x1,x2] |
|| φ1 2 ξ1 || || m1 || || f [x1,x2,x3] ||
|| ... ... ... || || ... || = 6 || . ||
|( φ 2 ξ |) |( m |) || .. ||
ξn− 1 − 1 φn−1 nm−1 ( f[xn−2,xn−1,xn])
n−1 n−1 n 0](relazione433x.png) |
Sommando la seconda riga alla prima e la penultima all’ultima si ottiene:
![( )
( 1 1 1 ) ( m0 + m1 ) | f[x0,x1,x2] |
|| φ1 2 ξ1 || || m1 || || f[x0,x1,x2] ||
|| .. .. .. || || .. || = 6 || f[x1,x2,x3] ||
| . . . | | . | || ... ||
( φn−1 2 ξn−1 ) ( mn −1 ) ( f [xn−2,xn−1,xn])
1 1 1 mn + mn−1 f [xn−2,xn−1,xn]](relazione434x.png) |
che ancora non è una matrice tridiagonale a causa degli elementi sottolineati. Possiamo però sottrarre la prima colonna dalla seconda e dalla terza e l’ultima dalla penultima e terzultima per ottenere finalmente una matrice tridiagonale. Per fare questo ci serviremo di una matrice siffatta:
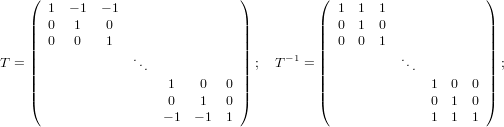 |
Quello che andremo a svolgere invece di Am = b diviene ATT−1m = b, e la matrice AT è quindi:
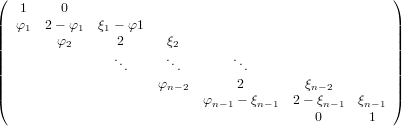 |
![( ) ( )
m0 + m1 + m2 f[x0,x1,x2]
|| m1 || || f[x0,x1,x2] ||
|| ... || = 6|| ... ||
|( m |) |( f[x ,x ,x ]|)
m + m n−1+ m f[xn−2,xn−1,x n]
n n−1 n−2 n−2 n−1 n](relazione437x.png) |
che è tridiagonale e fattorizzabile LU in quanto ha tutti i minori principali non nulli.
Per avere una spline completa invece dobbiamo imporre:
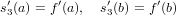 |
ovvero (considerando per comodità gli indici che partono da 1 anziché da 0 ed arrivano ad n, in accordo con quanto utilizzato nelle implementazioni):
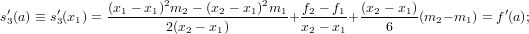 |
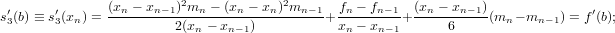 |
da cui si ottiene:
![′ ′
− 3h1m1+h1 (m2− m1) = 6f(a)− 6f[x1,x2]; 3hn−1mn+hn −1(mn − mn −1) = 6f (b)− 6f [xn,xn−1];](relazione441x.png) |
ovvero:
![− 4h1m1+h1m2 = 6(f′(a)− f[x1,x2]); 4hn−1mn − hn−1mn −1 = 6(f′(b)− f[xn−1,xn]).](relazione442x.png) |
Si ricava quindi la matrice:
![( )
( − 4h1 h1 ) ( m1 ) f′(a)− f[x1,x2]
|| φ1 2 ξ1 || || .. || || f[x1,x2] ||
|| φ2 2 ξ2 || || . || || ... ||
|| .. .. .. || || ... || = 6|| . ||
| . . . | | .. | || .. ||
( φn− 1 2 ξn−1 ) ( . ) ( f[x1,x2] )
− hn−1 4hn −1 mn f′(b)− f[xn−1,xn]](relazione443x.png) |
che ancora una volta è tridiagonale con tutti i minori principali non nulli, e pertanto fattorizzabile LU.
Per calcolare la spline cubica periodica invece dobbiamo imporre:
 |
Sostituendo nelle formule (come nel caso precedente per semplicità sono stati usati gli indici Matlab) andiamo a ricavare:
![(x2 − x1)m1 h1 (xn − xn−1)mn hn− 1
−-----2-----+f [x1,x2]− -6 (m2 − m1 ) =----2------+f [xn,xn−1]−--6--(mn − mn−1)](relazione445x.png) |
![− 3h1m1 − 3hn−1mn − h1(m2 − m1 )+ hn−1(mn − mn −1) = 6(f[xn,xn− 1]− f[x1,x2])](relazione446x.png) |
da cui otteniamo quindi la prima condizione:
![− 2h1m1 − 2hn−1mn − h1m2 − hn−1mn −1 = 6(f[xn,xn −1]− f [x1,x2]).](relazione447x.png) |
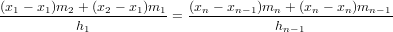 |
 |
Andiamo quindi a costruire la matrice relativa al sistema lineare risultante:
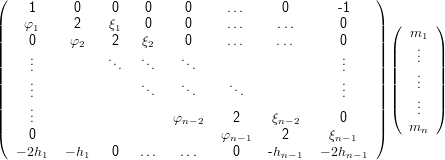 |
![( )
0
|| f [x1,x2] ||
|| ... ||
|| . ||
= 6|| .. ||
|| ... ||
|( f[x ,x ] |)
f[x ,x n]−n f−1[x − x ]
n n−1 1 2](relazione451x.png) |
Il problema che ci poniamo in questa sezione è quello di determinare il polinomio che meglio approssima una serie di dati sperimentali, i quali tipicamente sono in sovrabbondanza ma soggetti ad errori. Vogliamo quindi determinare un polinomio di grado m:
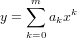 |
che meglio approssimi i dati:
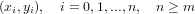 |
dove le ascisse non sono necessariamente tutte distinte, anche se dobbiamo imporre che nella determinazione di un polnomio in Πm, almeno m + 1 lo siano. Definiamo quindi i vettori f e y rispettivamente dei valori osservati e previsti:
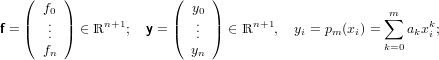 |
rimane da determinare il vettore a = (a0,a1,...,am)T che minimizza la quantità:
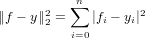 |
ovvero:
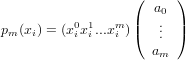 |
Possiamo esprimere quindi il problema in questa forma:
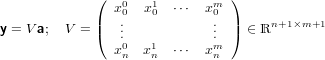 |
Si ha che:
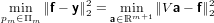 |
La matrice V ha rango m + 1.
Dimostrazione:
Se ci si limita a considerare m + 1 righe corrispondenti ad ascisse distinte, esse formano
una matrice di Vandermonde nonsingolare, e quindi il rango è appunto m + 1.
Il problema diventa quindi quello di risolvere, nel senso dei minimi quadrati, il sistema
sovradeterminato:
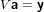 |
Possiamo quindi considerare:
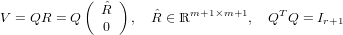 |
e quindi:
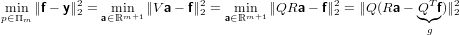 |
 |
Ne deriva quindi che la soluzione di questa equazione, a = 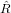 −1g1 esiste ed è unica, ed è
quindi tale anche il polinomio di approssimazione ai mini quadrati. Notiamo che nel
caso particolare in cui m = n, il polinomio di approssimazione ai minini quadrati
coincide esattamente con quello interpolante sulle stesse ascisse; in tal caso infatti il
vettore residuo g2 è il vettore vuoto e il polinomio quindi interpola tutti i valori
assegnati.
−1g1 esiste ed è unica, ed è
quindi tale anche il polinomio di approssimazione ai mini quadrati. Notiamo che nel
caso particolare in cui m = n, il polinomio di approssimazione ai minini quadrati
coincide esattamente con quello interpolante sulle stesse ascisse; in tal caso infatti il
vettore residuo g2 è il vettore vuoto e il polinomio quindi interpola tutti i valori
assegnati.
Può succedere di aver bisogno di minimizzare, invece della norma del vettore dei residui, un vettore pesato ∥D(V a −f∥22 che permetta appunto di dare un’importanza maggiore o minore a certe misurazione rispetto alle altre. Definiamo quindi:
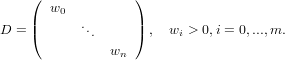 |
abbiamo quindi che:
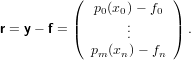 |
Quindi il problema:
 |
diventa:
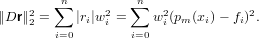 |
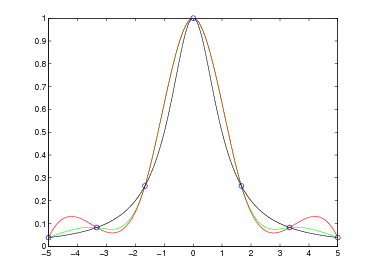
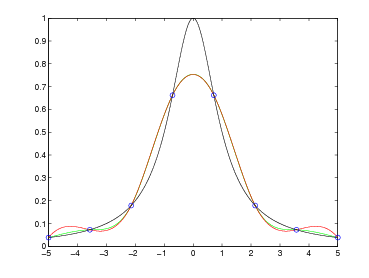
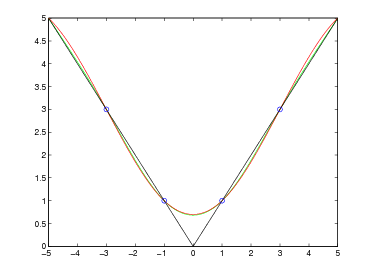
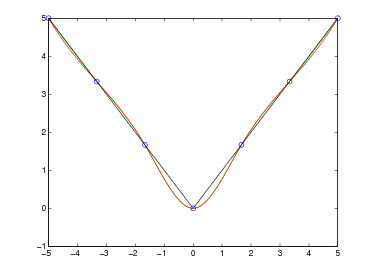
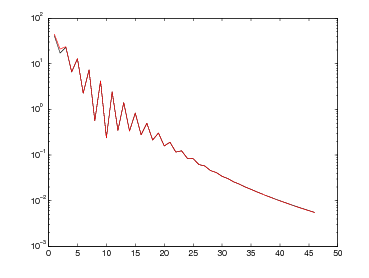
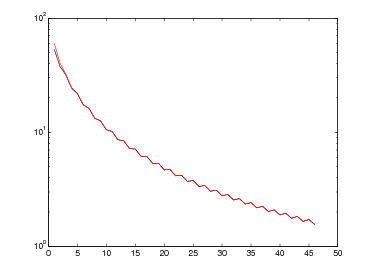
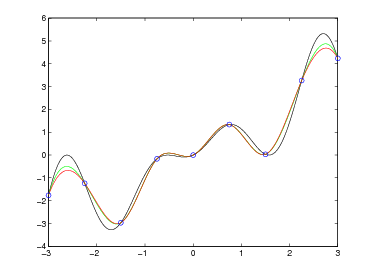
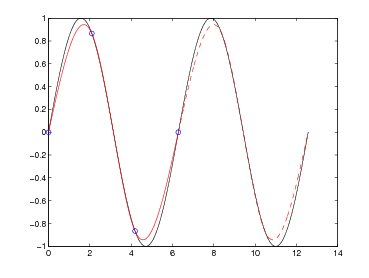
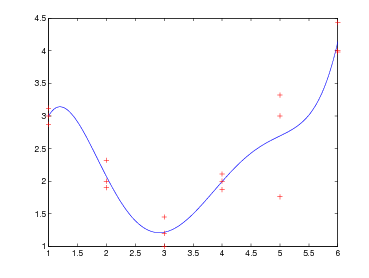
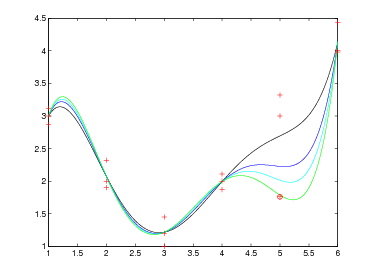
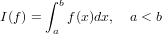 |
con [a,b] intervallo limitato, ed f(x) continua su tale intervallo. Per fare ciò andremo a calcolare l’integrale di una funzione polinomiale (o polinomiale a tratti) che approssimi fx), cosa che siamo in grado di fare in modo semplice e senza approssimazioni. Quello che adremo a fare sarà quindi calcolare:
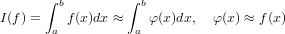 |
Studiamo adesso il condizionamento del problema:
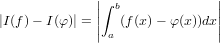 |
questa quantità può essere maggiorata con:
![∫ ∫
|I(f)− I(φ)| ≤ b|f (x) − φ (x )|dx ≤ max |f(x)− φ(x)| bdx
a x∈[a,b] a](relazione481x.png) |
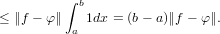 |
Il fattore (b − a) rappresenta quindi il fattore di amplificazione dell’errore sul risultato, e quindi:
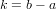 |
definisce il numero di condizinamento del problema.
Consideriamo l’approssimazione di f(x) fornita dal polinomio interpolante su n + 1 ascisse equidistanti:
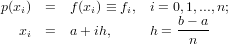 |
Se si considera la forma di Lagrange del polinomio interpolante si ottiene:
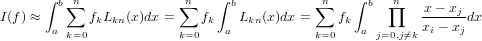 |
ponendo x = a + th, t = 0,...,n, si ottiene:
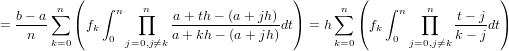 |
Abbiamo quindi ottenuto la formula che definisce l’approssimazione di I(f) che stavamo cercando:
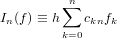 |
in cui
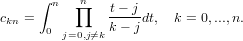 |
è detta formula di quadrtura di Newton-Cotes.
Per i coefficienti ckn vale che:
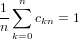 |
Dimostrazione:
considerando f(x) ≡ 1 si ha che:
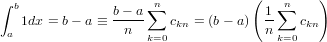 |
da cui deriva direttamente la tesi.
Poniamo n = 1. Sappiamo che c01 + c11 = 1, e quindi:
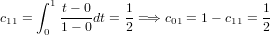 |
e quindi:
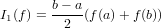 |
che approssima l’aria sottesa dal grafico di f(x) con quella sottesa dal trapezio di vertici (a,0),(a,f(a)),(b,f(b))(b,0).
Se invece poniamo n = 2, sappiamo che c02 + c12 + c22 = 2, pertanto:
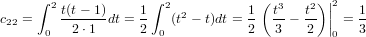 |
e
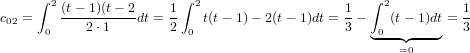 |
e si può ricavare c12 = 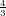 . Quindi:
. Quindi:
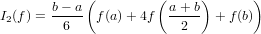 |
Questo è il codice che implementa quanto appena descritto:
Indichiamo con φ(x) la perturbazione della funzione f(x). Si ottiene:
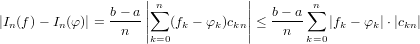 |
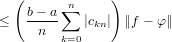 |
e quindi otteniamo che il numero di condizionamento del problema è:
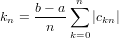 |
Osserviamo che :
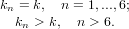 |
Ne consegue quindi che i problemi di calcolo I(f) e In(f) hanno lo stesso numero di condizionamento solo per n ≤ 6, e quindi le formule di Newton-Cotes sono sconvenienti al crescere di n.
Esaminiamo adesso l’errore di quadratura, definito in questo modo:
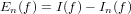 |
Dall’espressione dell’errore di interpolazione discende che:
![∫ b ∫ b ∫ b
En(f) = a e(x)dx = a (f(x)− pn(x))dx = a f[x0,...,xn,x ]ωn+1(x)dx.](relazione502x.png) |
Se f(x) ∈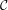 (n+k), con
(n+k), con
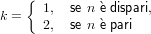 |
allora l’errore di quadratura è dato da:
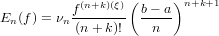 |
per un opportuno ξ ∈ [a,b], ed:
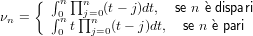 |
Per il metodo dei trapezi si ottiene quindi :
![1
E1(f) = −--f(2)(ξ)(b− a)3, ξ ∈ [a,b]
12](relazione506x.png) |
e per quello di simpson:
![1 (4) (b− a )5
E2 (f ) = − 90f (ξ) --2-- , ξ ∈ [a,b]](relazione507x.png) |
Per ridurre il rapporto (b − a)∕n, è possibile pensare di suddividere l’intervallo [a,b] in più
sottointervalli della medesima ampiezza, ed utilizzare la stessa dormula di Newton-Cotes per
ciascun sottointervallo.
Consideriamo l’applicazione della formula dei trapezi su ciascun sottointervallo [xi−1,xi],i = 1,...,n di una partizione uniforme di [a,b]:
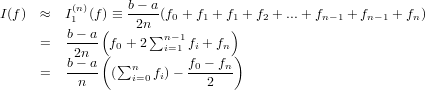 |
Il cui errore di quadratura vale:
![(n) n (2) ( b− a)3
E 1 (f) = − 12f (ξ) -n--- , ξ ∈ [a,b].](relazione509x.png) |
Considerando solo valori pari di n:
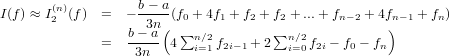 |
ed il corrispondente errore di quadratura:
![(n) n ( b− a)
E2 (f) = −180f(4)(ξ) -n--- ,ξ ∈ [a,b]](relazione511x.png) |
Notiamo come, per n →∞, Ek(n) → 0 con k = 1,2.
Questo codice implementa la formula dei trapezi e quella di Simpson composite:
Non è infrequente che la funzione integranda f(x) abbia delle variazioni rapide solo in uno o più piccoli sottointervalli dell’intervallo [a.b], e al contempo sia molto regolare negli altri tratti. Quello che si vuole ottenere in questi casi è un metodo che si sappia adattare automaticamente a questo tipo di situazioni, ovvero che permetta di scegliere in modo opportuno i nodi della partizione dell’intervallo [a,b].
applicando il metodo dei trapezi sull’intervallo [a,b] diviso in 1 e 2 sottointervalli si ha:
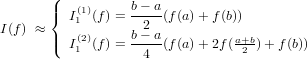 |
ovvero:
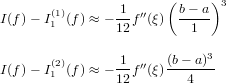 |
facendo la differenza membro a membro si ottiene:
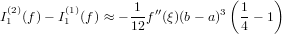 |
e ancora dividendo per −3:
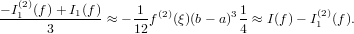 |
Abbiamo appena trovato una stima dell’errore:
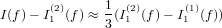 |
che possiamo utilizzare come soglia in un algoritmo ricorsivo per decidere se è il caso di suddividere ulteriormente il sottointervallo considerato.
applicando il metodo di Simpson sull’intervallo [a,b] diviso in 2 e 4 sottointervalli si ha:
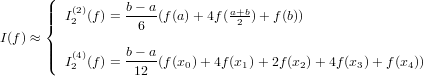 |
dove x0 = a,x2 = 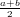 ,x4 = b,x1 =
,x4 = b,x1 = 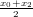 ,x3 =
,x3 = 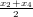 .
.
Si ottiene quindi:
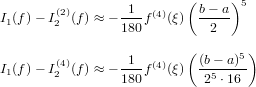 |
da cui:
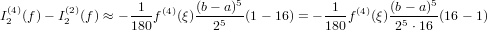 |
Abbiamo appena trovato una stima dell’errore:
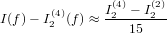 |
che come nel caso della formula dei trapezi possiamo utilizzare come soglia per decidere se è il caso di suddividere ulteriormente il sottointervallo considerato.
Questi codici implementano in maniera ricorsiva e molto semplice le formule adattive dei trapezi e di Simpson:
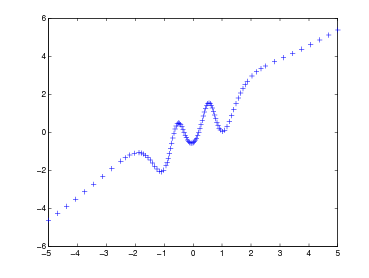
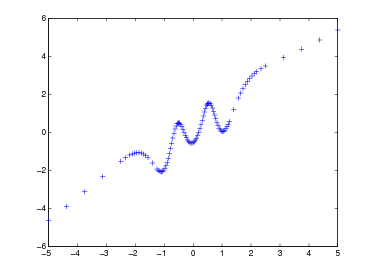
Questo metodo, invece di richiedere la formula della derivata prima come fa il metodo originale, calcola un’approssimazione del valore di questa nel punto iniziale x0:
Cercando uno zero della funzione f(x) = x3 + sin(10x):
| x0 | tolx | iter.S | ris. Secanti | iter.SM | ris. Sec. Mod. | errore |
| 0.2 | 10−2 | 2 | 0.31674403271112 | 2 | 0.31674403804563 | 5e-09 |
| 0.2 | 10−6 | 4 | 0.31735605718908 | 4 | 0.31735605718908 | 1e-15 |
| 0.2 | 10−10 | 5 | 0.31735605713204 | 5 | 0.31735605713204 | 5e-17 |
| 1.5 | 10−2 | 15 | -0.31053322118703 | 17 | -0.31735615577029 | 6e-3 |
| 1.5 | 10−4 | 18 | -0.31735605713204 | 18 | -0.31735605713245 | 4e-13 |
| 1.5 | 10−10 | 19 | -0.31735605713204 | 19 | -0.31735605713204 | 5e-17 |
| 1.06 | 10−2 | 47 | -8.549970108032228e-06 | 25 | 0.31666506455617 | - |
| 1.06 | 10−4 | 49 | -8.844156346925046e-21 | 27 | 0.31735605728114 | - |
| 1.06 | 10−10 | 49 | -8.844156346925046e-21 | 29 | 0.31735605713204 | - |
Vediamo quindi che la valutazione approssimata della derivata porta in un caso a convergere verso una radice diversa rispetto a quella cui converge il metodo originale (ma comunque è un risultato corretto), e negli altri casi non peggiora il risultato.
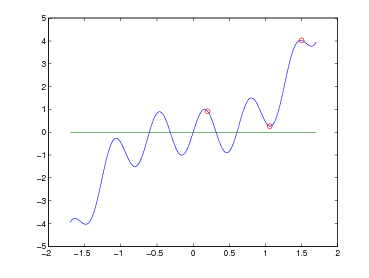
Questa è la versione ottimizzata dell’algoritmo presentato nella parte teorica. Con queste semplici modifiche si riesce ad ottenere un aumento di prestazioni notevole: fattorizzando una matrice di elementi random di 2000x2000 elementi, si passa dai 195.73 secondi dell’algoritmo originale a 74.32.
Con questo algoritmo si recuperano dalla matrice A restituita dall’algoritmo di fattorizzazione i fattori L ed U necessari alla effettiva risoluzione del sistema:
Questo semplice codice automatizza la risoluzione del sistema Ax = b:
In caso si debba fattorizzare un sistema tridiagonale si può migliorare l’algoritmo:
Questa versione ottimizzata dell’algoritmo presentato nella parte teorica utilizza un vettore contenente la porzione triangolare inferiore della matrice A anziché tutta la matrice, sfruttandone la simmetria. Il codice può essere ulteriormente ottimizzato integrando le funzionalità dei metodi vget e vstore nel codice; viene effettuata una chiamata al metodo per ogni accesso ad un elemento della matrice, e questo appesantisce parecchio dal punto di vista computazionale (ma facilita la lettura del codie).
Questo codice serve per vettorizzare per righe la porzione triangolare inferiore di una matrice:
Questa è un’ottimizzazione del codice di vettorizzazione:
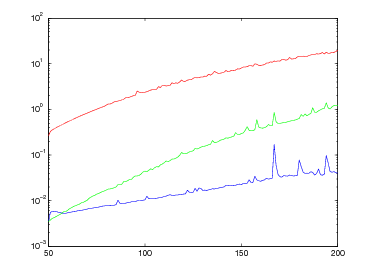
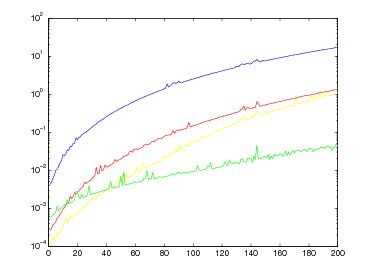
Questa versione del metodo elimina le chimate di funzione per il calcolo degli indici:
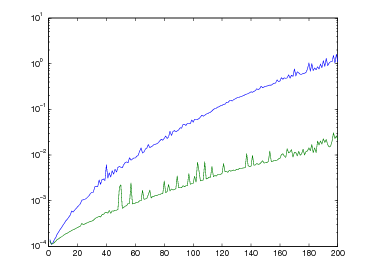
Con questo algoritmo si recuperano dalla matrice A restituita dall’algoritmo di fattorizzazione non ottimizzato i fattori L e D necessari alla effettiva risoluzione del sistema:
E con questo si fa la stessa cosa a partire dal vettore restituito dalla versione vettorizzata:
Questo semplice codice automatizza la risoluzione del sistema Ax = b:
Come nel caso della fattorizzazione LU, svolgendo a mano i cicli che Matlab svolge in maniera inefficiente guadagnamo del tempo:
Questo codice automatizza la risoluzione del sistema Ax = b:
in cui utilizziamo il metodo di permutazione:
Con questo algoritmo recuperiamo i fattori Q′ ed R direttamente utili alla risoluzione del
sistema; l’algoritmo di fattorizzazione restituisce nella porzione triangolare inferiore della
matrice i vettori di Householder ed è pertanto necessario calcolare la matrice Q′, R è
facilmente costruibile a partire da 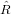 .
.
Anche in questo caso abbiamo un semplice codice per automatizzare la risoluzione del sistema Ax = b:
Questo algoritmo valuta il polinomio p(x) = ∑ k=0nakxk nei punti contenuti nel vettore x a partire dal vettore a contenente i coefficienti del polinomio. Quello che si fa infatti è svolgere il calcolo: a1 + x(a2 + x(a3 + x(...anx))) che svolgendo i calcoli si vede essere equivalente a: a1 + xa2 + x2a3 + ... + xnan.
Questo algoritmo valuta il polinomio p(x) = a1+(x−x1)a2+(x−x1)(x−x2)a3+...+(x−x1)...(x−xn−1)an nei punti contenuti nel vettore x0 a partire dal vettore a contenente i coefficienti del polinomio e il vettore x contenente le radici del polinomio.
Questo semplice codice calcola e valuta una spline lineare:
Questi codici effettuano il calcolo e la valutazione in un array di punti di una spline cubica naturale:
Questi codici effettuano il calcolo e la valutazione in un array di punti di una spline cubica con condizioni not-a-knot:
Questi codici effettuano il calcolo e la valutazione in un array di punti di una spline cubica Completa:
Questi codici effettuano il calcolo e la valutazione in un array di punti di una spline cubica Periodica:
Qusto codice calcola e valuta il polinomio che risolve il problema dei minimi quadrati: